
【题目】如图,已知△ABC内接于⊙O,AB为⊙O的直径,BD⊥AB,交AC的延长线于点D.
(1)E为BD的中点,连结CE,求证:CE是⊙O的切线;
(2)若AC=3CD,求∠A的大小.
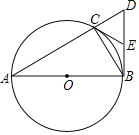
【答案】(1)见解析;(2)∠A=30°.
【解析】
(1)连接OC,根据等腰三角形的性质得到∠A=∠1,根据三角形的中位线的性质得到OE∥AD,从而得到∠2=∠3,然后证出△COE≌△BOE,根据全等三角形的性质得到∠OCE=∠ABD=90°,于是得到CE是⊙O的切线;
(2)由AB为⊙O的直径,得到BC⊥AD,根据相似三角形的性质得到BC2=ACCD,再根据AC=3CD,得到tanA=![]() ,于是得到结论.
,于是得到结论.
解:(1)连接OC,
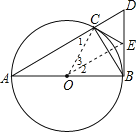
∵BD⊥AB,∴∠ABD=90°,
∵OA=OC,
∴∠A=∠1,
∵AO=OB,E为BD的中点,
∴OE∥AD,
∴∠1=∠3,∠A=∠2,
∴∠2=∠3,
在△COE与△BOE中,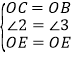 ,
,
∴△COE≌△BOE,
∴∠OCE=∠ABD=90°,
∴CE是⊙O的切线;
(2)∵AB为⊙O的直径,
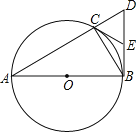
∴∠ACB=90°,
∵AB⊥BD,∴∠ABD=∠ACB=90°,
∴∠A+∠ABC=90°,∠ABC+∠CBD=90°
∴∠A=∠CBD,
∴△ABC∽△BDC,
∴![]() ,
,
∴BC2=ACCD,
∵AC=3CD,
∴BC2=![]() AC2,
AC2,
∴在R![]() 中,tanA=
中,tanA=![]() ,
,
∴∠A=30°


科目:初中数学 来源: 题型:
【题目】阅读材料:求31+32+33+34+35+36的值
解:设S=31+32+33+34+35+36①
则3S=32+33+34+35+36+37②
用②﹣①得,3S﹣S=(32+33+34+35+36+37)﹣(31+32+33+34+35+36)=37﹣3
∴2S=37﹣3,即S=![]() ,∴31+32+33+34+35+36=
,∴31+32+33+34+35+36=![]()
以上方法我们成为“错位相减法”,请利用上述材料,解决下列问题:
(一)棋盘摆米
这是一个很著名的故事:阿基米德与国王下棋,国王输了,国王问阿基米德要什么奖赏?阿基米德对国王说:“我只要在棋盘上第一格放一粒米,第二格放二粒,第三格放四粒,第四格放八粒…按这个方法放满整个棋盘就行”国王以为要不了多少粮食,就随口答应了,结果国王输了
(1)国际象棋共有64个格子,则在第64格中应放 粒米(用幂表示)
(2)设国王输给阿基米德的米粒数为S,求S
(二)拓广应用:
1.计算:![]() (仿照材料写出求解过程)
(仿照材料写出求解过程)
2.计算:![]() = (直接写出结果)
= (直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了以“责任、感恩”为主题的班队活动,活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图,

(1)该班有 人,学生选择“和谐”观点的有 人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是 度;
(2)如果该校有360名初三学生,利用样本估计选择“感恩”观点的初三学生约有 人;
(3)如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查,求恰好选到“和谐”和“感恩”观点的概率(用树状图或列表法分析解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
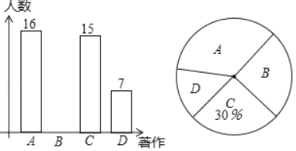
【题目】某校对A《唐诗》、B《宋词》、C《蒙山童韵》、D其它,这四类著作开展“最受欢迎的传统文化著作”调查,随机调查了若干名学生(每名学生必选且只能选这四类著作中的一种)并将得到的信息绘制了下面两幅不完整的统计图:
(1)求一共调查了多少名学生;
(2)请将条形统计图补充完整;
(3)该校语文老师想从这四类著作中随机选取两类作为学生寒假必读书籍,请用树状图或列表的方法求恰好选中《宋词》和《蒙山童韵》的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
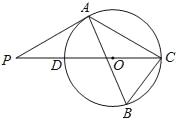
【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
(1)求证:PA是⊙O的切线;
(2)若AB=4+![]() ,BC=2
,BC=2![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,O是AB上一点,以OA为半径的⊙O与BC相切于点D,与AB交于点E,连接ED并延长交AC的延长线于点F.
(1)求证:AE=AF;
(2)若DE=3,sin∠BDE=![]() ,求AC的长.
,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() .点
.点![]() 为
为![]() 轴上一动点,过点
轴上一动点,过点![]() 且垂直于
且垂直于![]() 轴的直线分别交直线
轴的直线分别交直线![]() 及抛物线于点
及抛物线于点![]() ,
,![]() .
.
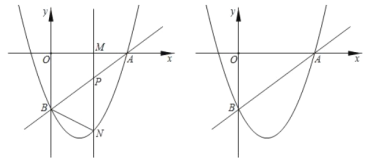
(1)填空:点![]() 的坐标为_________,抛物线的解析式为_________;
的坐标为_________,抛物线的解析式为_________;
(2)当点![]() 在线段
在线段![]() 上运动时(不与点
上运动时(不与点![]() ,
,![]() 重合),
重合),
①当![]() 为何值时,线段
为何值时,线段![]() 最大值,并求出
最大值,并求出![]() 的最大值;
的最大值;
②求出使![]() 为直角三角形时
为直角三角形时![]() 的值;
的值;
(3)若抛物线上有且只有三个点![]() 到直线
到直线![]() 的距离是
的距离是![]() ,请直接写出此时由点
,请直接写出此时由点![]() ,
,![]() ,
,![]() ,
,![]() 构成的四边形的面积.
构成的四边形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=﹣![]() x2+2
x2+2![]() x﹣
x﹣![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,顶点为D,对称轴与x轴交于点E,直线CE交抛物线于点F(异于点C),直线CD交x轴交于点G.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,顶点为D,对称轴与x轴交于点E,直线CE交抛物线于点F(异于点C),直线CD交x轴交于点G.
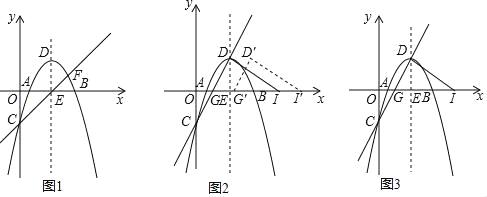
(1)如图1,求直线CE的解析式和顶点D的坐标;
(2)如图1,点P为直线CF上方抛物线上一点,连接PC、PF,当△PCF的面积最大时,点M是过P垂直于x轴的直线l上一点,点N是抛物线对称轴上一点,求FM+MN+NO的最小值;
(3)如图2,过点D作DI⊥DG交x轴于点I,将△GDI沿射线GB方向平移至△G′D′I′处,将△G′D′I′绕点D′逆时针旋转α(0<α<180°),当旋转到一定度数时,点G′会与点I重合,记旋转过程中的△G′D′I′为△G″D′I″,若在整个旋转过程中,直线G″I″分别交x轴和直线GD′于点K、L两点,是否存在这样的K、L,使△GKL为以∠LGK为底角的等腰三角形?若存在,求此时GL的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读例题,回答问题:
例题:已知二次三项式:x2﹣4x+m有一个因式是x+3,求另一个因式以及m的值.
解:设另一个因式为x+n,得x2﹣4x+m=(x+3)(x+n),则x2﹣4x+m=x2+(n+3)x+3n.
∴![]()
∴![]()
∴另一个因式为x﹣7,m=21.
仿照以上方法解答下面的问题:
已知二次三项式2x2+3x+k有一个因式是2x﹣5,求另一个因式以及k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com