
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�������y����![]() x2+2
x2+2![]() x��
x��![]() ��x�ύ��A��B����(��A�ڵ�B�����)����y�ύ�ڵ�C������ΪD���Գ�����x�ύ�ڵ�E��ֱ��CE���������ڵ�F(���ڵ�C)��ֱ��CD��x�ύ�ڵ�G��
��x�ύ��A��B����(��A�ڵ�B�����)����y�ύ�ڵ�C������ΪD���Գ�����x�ύ�ڵ�E��ֱ��CE���������ڵ�F(���ڵ�C)��ֱ��CD��x�ύ�ڵ�G��
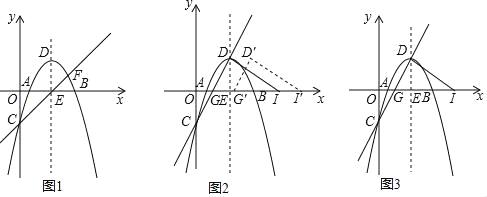
(1)��ͼ1����ֱ��CE�Ľ���ʽ�Ͷ���D�����ꣻ
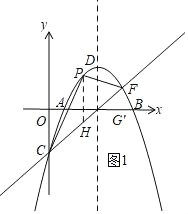
(2)��ͼ1����PΪֱ��CF�Ϸ���������һ�㣬����PC��PF������PCF��������ʱ����M�ǹ�P��ֱ��x���ֱ��l��һ�㣬��N�������߶Գ�����һ�㣬��FM+MN+NO����Сֵ��
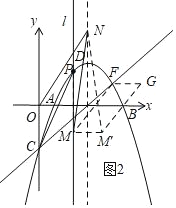
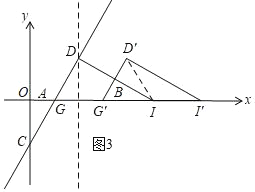
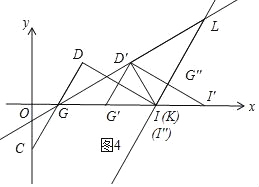
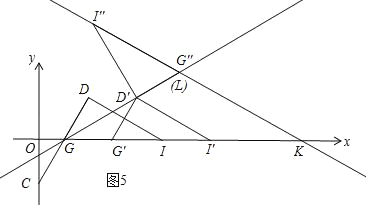
(3)��ͼ2������D��DI��DG��x���ڵ�I������GDI������GB����ƽ������G��D��I����������G��D��I���Ƶ�D����ʱ����ת��(0������180��)������ת��һ������ʱ����G�������I�غϣ�����ת�����еġ�G��D��I��Ϊ��G��D��I��������������ת�����У�ֱ��G��I���ֱ�x���ֱ��GD���ڵ�K��L���㣬�Ƿ����������K��L��ʹ��GKLΪ�ԡ�LGKΪ�ǵĵ��������Σ������ڣ����ʱGL�ij���
���𰸡�(1) D(2��![]() )��y��
)��y��![]() x��
x��![]() ��(2)
��(2)![]() ��(3)���ڣ�GL�ij�Ϊ4
��(3)���ڣ�GL�ij�Ϊ4![]() ��2
��2![]() +2��
+2��
��������
��1�����������߽���ʽ��õ�C�͵�D�����꣬�ٸ��������߶Գ�����õ�E�����꣬���ô���ϵ�������CE�Ľ���ʽ.
��2�������������F������꣬��P��PH��x�ᣬ��CE��H�� ��P(a����![]() a2+2
a2+2![]() a��
a��![]() ) ��H(a��
) ��H(a��![]() a��
a��![]() )����PH����PCF�������ʾ���������ݶ��κ���ͼ������ʿɵ���PCF��������ֵ.����M���ڶԳ���ĶԳƵ�M'����F����FG��MM'����֤FGM'M��ƽ���ı��Σ�FM+MN+ON��GM'+NM'+ON��
)����PH����PCF�������ʾ���������ݶ��κ���ͼ������ʿɵ���PCF��������ֵ.����M���ڶԳ���ĶԳƵ�M'����F����FG��MM'����֤FGM'M��ƽ���ı��Σ�FM+MN+ON��GM'+NM'+ON��
��������֮���߶���̿�֪����O��N��M'��G�ĵ㹲��ʱ��GM'+NM'+ON��ֵ��̣��� FM+MN+ON��ֵ��С��������ֵ�������.
��3���ô���ϵ�������ֱ��CD�ĺ�������ʽ�����G�������DG�ij��ȣ�����ת��һ������ʱ����G�������I�غϣ�����D'I��֤����G'D'I�ǵȱ������Σ���������ۼ��ɵõ�GL�ij�.
�⣺(1)��������y����![]() x2+2
x2+2![]() x��
x��![]() ��y�ύ�ڵ�C��
��y�ύ�ڵ�C��
��C(0����![]() )��
)��
��y����![]() x2+2
x2+2![]() x��
x��![]() ����
����![]() (x��2)2+
(x��2)2+![]() ��
��
�ඥ��D(2��![]() )���Գ���x��2��
)���Գ���x��2��
��E(2��0)��
��CE����ʽy��kx+b��
��![]() ��
��
��ã�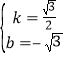 ��
��
��ֱ��CE�Ľ���ʽ��y��![]() x��
x��![]() ��
��
(2) ��ֱ��CE���������ڵ�F(���ڵ�C)��
��![]() x��
x��![]() ����
����![]() (x��2)2+
(x��2)2+![]() ��
��
��x1��0��x2��3��
��F(3��![]() )��
)��
��P��PH��x�ᣬ��CE��H����ͼ1��
��P(a����![]() a2+2
a2+2![]() a��
a��![]() ) ��H(a��
) ��H(a��![]() a��
a��![]() )��
)��
��PH����![]() a2+2
a2+2![]() a��
a��![]() ��(
��(![]() a��
a��![]() )��
)��
����![]() a2+
a2+![]() ��
��
��S��CFP��![]() PH��3����
PH��3����![]() a2+
a2+![]() ��
��
�൱a��![]() ʱ��S��CFP������
ʱ��S��CFP������
����M���ڶԳ���ĶԳƵ�M'����F����FG��MM'��FG��1����G(4��![]() )����ͼ2
)����ͼ2
��M�ĺ�����Ϊ![]() ����M��M'���ڶԳ���x��2�Գƣ�
����M��M'���ڶԳ���x��2�Գƣ�
��M'�ĺ�����Ϊ![]() ��
��
��MM'��1��
��MM'��FG����FG��MM'��
��FGM'M��ƽ���ı��Σ�
��FM��GM'��
��FM+MN+ON��GM'+NM'+ON��
��������֮���߶���̿�֪����O��N��M'��G�ĵ㹲��ʱ��GM'+NM'+ON��ֵ��̣��� FM+MN+ON��ֵ��С��
��FM+MN+ON��OG��![]() ��
��![]() ��
��
(3)��ͼ3����CD����ʽy��mx+n����![]() ��
��
��ã�![]() ��
��
��CD����ʽy��![]() x��
x��![]() ��
��
�൱y��0ʱ��x��1����G(1��0)��
��DG��![]() ��2��
��2��
��tan��DGI��![]() ��
��![]() ��
��
���DGI��60����
��DI��DG��
���GDI��90������GID��30����
��GI��2DG��4
��I(5��0)��
�߽���GDI������GB����ƽ������G��D��I����������G��D��I���Ƶ�D����ʱ����ת��(0������180��)������ת��һ������ʱ����G�������I�غϣ�����D'I��
��G'D'��D'I��DG��2����D'G'I����DGI��60����
���G'D'I�ǵȱ������Σ�
��G'I��2��G'K��2D'G'��4
��G'(3��0)��
��ͼ4����I'��I��K�غϣ���GKLΪ�ԡ�LGKΪ�ǵĵ��������Σ���LGK����GLK��30����
��GL��D'G+D'L��4![]() ��
��
��ͼ5��L��G'�غϣ���GKLΪ�ԡ�LGKΪ�ǵĵ��������Σ�
��GL��GD'+D'L��2![]() +2
+2
���ϣ�GL�ij�Ϊ4![]() ��2
��2![]() +2��
+2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD��ƽ��ֱ������ϵ�ĵ�һ�����ڣ�BC��x��ƽ�У�AB=1����C������Ϊ��6��2����E��AD���е㣻����������y1=![]() ��x��0��ͼ����C�͵�E������B��ֱ��y2=ax+b�뷴��������ͼ���ڵ�F����F��������Ϊ4��
��x��0��ͼ����C�͵�E������B��ֱ��y2=ax+b�뷴��������ͼ���ڵ�F����F��������Ϊ4��
��1�����������Ľ���ʽ�͵�E�����ꣻ
��2����ֱ��BF�Ľ���ʽ��
��3��ֱ��д��y1��y2ʱ���Ա���x��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
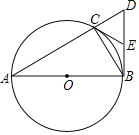
����Ŀ����ͼ����֪��ABC�ڽ��ڡ�O��ABΪ��O��ֱ����BD��AB����AC���ӳ����ڵ�D��
��1��EΪBD���е㣬����CE����֤��CE�ǡ�O�����ߣ�
��2����AC��3CD�����A�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij�칫¥AB�ĺ�����һ������CD�������������ļн���22��ʱ���칫¥�ڽ������ǽ�����¸�3��Ӱ��CE���������������н���45��ʱ���칫¥��A�ڵ����ϵ�Ӱ��F��ǽ��C��27�ľ��루B��F��C��һ��ֱ���ϣ���

��1����칫¥AB�ĸ߶ȣ�
��2����Ҫ��A��E֮���һЩ���죬�������A��E֮��ľ��룮
���ο����ݣ�sin22����![]() ��cos22����
��cos22����![]() ��tan22����
��tan22����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
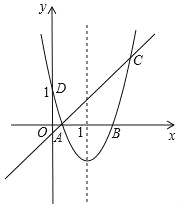
����Ŀ����ͼ��һ�κ���y1��x��![]() ��x�ύ��Aǡ���Ƕ��κ���y2��x�������һ�����㣬��֪���κ���ͼ��ĶԳ���Ϊx��1������y��Ľ���ΪD(0��1)��
��x�ύ��Aǡ���Ƕ��κ���y2��x�������һ�����㣬��֪���κ���ͼ��ĶԳ���Ϊx��1������y��Ľ���ΪD(0��1)��
(1)����κ����Ľ���ʽ��
(2)��ö��κ�����һ�κ�������һ������ΪC�㣬����DC����������ADC�������
(3)����ͼ��ֱ��д����y1��y2ʱx��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2015��2��27�գ�������ȫ����ĸ��쵼С���ʮ�λ����ϣ�����ͨ���ˡ��й�����ĸ����巽���������Ƹĸ�����ĸУ����ȳ�Ϊ�ĸ�����㣮���������棬��Ϊ�������ˮƽ�����������й��������������Ѿ������12����ͷ���г������Ѿ�����������Ĺ�ע��ͼ9��ijһ���ֹ�����ڶ��ֱ������ӵĻ���ͳ��ͼ��

(1)����ͼ������������_____֧�г���Ӳ�����
(2)��ȫͼһ�е�����ͳ��ͼ��
(3)���������������ʤһ����3�֣�ƽһ����1�֣���һ����0�֣����÷������Ϊ�ھ��������ڶ��ֱ��������λ��ǰ4���ķֱ���A��49�֣�B��49�֣�C��48�֣�D��45�֣������һ�ֵı����У����Ƿֱ�͵�4���Ժ����ӽ��б�������֪���Ѿ�������һ�������У�A�ӺͶ��ִ�ƽ�������б�������״ͼ�ķ���������C�Ӷ�ùھ��ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
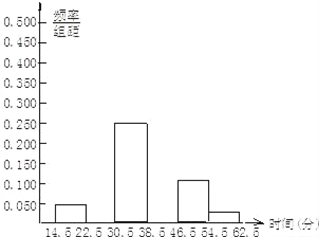
����Ŀ��ijУΪ���˽�ȫУ400��ѧ���μӿ������������������40��ѧ��һ����ƽ��ÿ��μӿ��������ʱ������˵��飬������£�(��λ����)
40 21 35 24 40 38 23 52 35 62 36 15 51 45 40 42 40 32 43 36
34 53 38 40 39 32 45 40 50 45 40 40 26 45 40 45 35 40 42 45
(1)��ȫƵ�ʷֲ�����Ƶ�ʷֲ�ֱ��ͼ��
���� | Ƶ�� | Ƶ�� |
4.5��22.5 | 2 | 0.050 |
22.5��30.5 | 3 | |
30.5��38.5 | 10 | 0.250 |
38.5��46.5 | 19 | |
46.5��54.5 | 5 | 0.125 |
54.5��62.5 | 1 | 0.025 |
�ϼ� | 40 | 1.000 |
(2)��գ�����������У�������____��������____����ͳ�ƽ�������ģ��������ݵ�ƽ������38.35(��)��������____����λ����_____��
(3)���������У400��ѧ��һ����ƽ��ÿ��μӿ������ʱ����������������Ϊ��ƽ��������������λ���е���һ�����ȽϺ��ʣ�
(4)��������ѧУ�ж�����ѧ����ƽ��ÿ��μӿ��������ʱ�����30�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
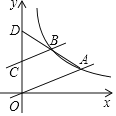
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() ��˫����
��˫����![]() ���ڵ�A������
���ڵ�A������![]() ��AO��ƽ���߽�˫�����ڵ�B������AB���ӳ���y�ύ�ڵ�
��AO��ƽ���߽�˫�����ڵ�B������AB���ӳ���y�ύ�ڵ�![]() ����k��ֵΪ______��
����k��ֵΪ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
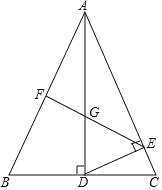
����Ŀ����ͼ���ڡ�ABC�У�AB��AC��AD��BC��D����DE��AC��E��F��AB�е㣬��EF��AD�ڵ�G��
(1)��֤��AD2��ABAE��
(2)��AB��3��AE��2����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com