
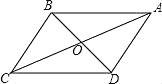
【题目】已知平行四边形ABCD中,如图,对角线AC和BD相交于点O,AC=10,BD=8.
(1)若AC⊥BD,试求四边形ABCD的面积;
(2)若AC与BD的夹角∠AOD=60°,求四边形ABCD的面积.
【答案】(1)S菱形ABCD=40;(2)S四ABCD=20![]()
【解析】
(1)先证平行四边形ABCD是菱形,根据菱形的面积公式即可求解;
(2)过点A分别作AE⊥BD,垂足为E,根据三角函数即可求得AE的长,从而求得△OAD的面积,四边形ABCD的面积是三角形OAD的面积的4倍,据此即可求解.
解:(1)∵AC⊥BD,
∴平行四边形ABCD为菱形,
∴S菱形ABCD=![]() AC×BD=40;
AC×BD=40;
(2)过点A分别作AE⊥BD,垂足为E,
∵四边形ABCD为平行四边形,
∴AO=CO=![]() AC=5,BO=DO=
AC=5,BO=DO=![]() BD=4,
BD=4,
在Rt△AOE中,sin∠AOE=![]() ,
,
∴AE=AOsin∠AOE=AO×sin60°=![]() ,
,
∴S四ABCD=![]() ODAE×4=
ODAE×4=![]() ×4×
×4×![]() ×4=20
×4=20![]() .
.

故答案为:(1)S菱形ABCD=40;(2)S四ABCD=20![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】随着北京申办冬奥会的成功,愈来愈多的同学开始关注我国的冰雪体育项目. 小健从新闻中了解到:在2018年平昌冬奥会的短道速滑男子500米决赛中,中国选手武大靖以39秒584的成绩打破世界纪录,收获中国男子短道速滑队在冬奥会上的首枚金牌. 同年11月12日,武大靖又以39秒505的成绩再破世界纪录. 于是小健对同学们说:“2022年北京冬奥会上武大靖再获金牌的可能性大小是![]() .”你认为小健的说法_________(填“合理”或“不合理”),理由是__________________________.
.”你认为小健的说法_________(填“合理”或“不合理”),理由是__________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:求31+32+33+34+35+36的值
解:设S=31+32+33+34+35+36①
则3S=32+33+34+35+36+37②
用②﹣①得,3S﹣S=(32+33+34+35+36+37)﹣(31+32+33+34+35+36)=37﹣3
∴2S=37﹣3,即S=![]() ,∴31+32+33+34+35+36=
,∴31+32+33+34+35+36=![]()
以上方法我们成为“错位相减法”,请利用上述材料,解决下列问题:
(一)棋盘摆米
这是一个很著名的故事:阿基米德与国王下棋,国王输了,国王问阿基米德要什么奖赏?阿基米德对国王说:“我只要在棋盘上第一格放一粒米,第二格放二粒,第三格放四粒,第四格放八粒…按这个方法放满整个棋盘就行”国王以为要不了多少粮食,就随口答应了,结果国王输了
(1)国际象棋共有64个格子,则在第64格中应放 粒米(用幂表示)
(2)设国王输给阿基米德的米粒数为S,求S
(二)拓广应用:
1.计算:![]() (仿照材料写出求解过程)
(仿照材料写出求解过程)
2.计算:![]() = (直接写出结果)
= (直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抚顺某中学为了解八年级学生的体能状况,从八年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级.请根据两幅统计图中的信息回答下列问题:
(1)本次抽样调查共抽取了多少名学生?
(2)求测试结果为C等级的学生数,并补全条形图;
(3)若该中学八年级共有700名学生,请你估计该中学八年级学生中体能测试结果为D等级的学生有多少名?
(4)若从体能为A等级的2名男生2名女生中随机的抽取2名学生,做为该校培养运动员的重点对象,请用列表法或画树状图的方法求所抽取的两人恰好都是男生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为直线x=﹣1,给出以下结论,①ab<0,②b2﹣4ac>0,③4b+c<0,④若B(﹣![]() ,y1)、C(﹣
,y1)、C(﹣![]() ,y2)为函数图象上的两点,则y1>y2,⑤当﹣3≤x≤1时,y≥0,其中正确的结论是( )
,y2)为函数图象上的两点,则y1>y2,⑤当﹣3≤x≤1时,y≥0,其中正确的结论是( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
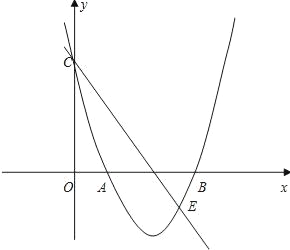
【题目】如图,已知二次函数y=ax2+bx+c的图象经过A(1,0)、B(5,0)、C(0,5)三点.
(1)求这个二次函数的解析式;
(2)过点C的直线y=kx+b与这个二次函数的图象相交于点E(4,m),请求出△CBE的面积S的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了以“责任、感恩”为主题的班队活动,活动结束后,初三(2)班数学兴趣小组提出了5个主要观点并在本班学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图,

(1)该班有 人,学生选择“和谐”观点的有 人,在扇形统计图中,“和谐”观点所在扇形区域的圆心角是 度;
(2)如果该校有360名初三学生,利用样本估计选择“感恩”观点的初三学生约有 人;
(3)如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查,求恰好选到“和谐”和“感恩”观点的概率(用树状图或列表法分析解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() .点
.点![]() 为
为![]() 轴上一动点,过点
轴上一动点,过点![]() 且垂直于
且垂直于![]() 轴的直线分别交直线
轴的直线分别交直线![]() 及抛物线于点
及抛物线于点![]() ,
,![]() .
.
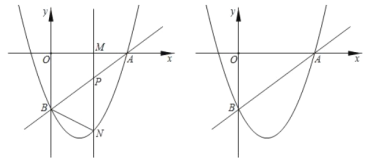
(1)填空:点![]() 的坐标为_________,抛物线的解析式为_________;
的坐标为_________,抛物线的解析式为_________;
(2)当点![]() 在线段
在线段![]() 上运动时(不与点
上运动时(不与点![]() ,
,![]() 重合),
重合),
①当![]() 为何值时,线段
为何值时,线段![]() 最大值,并求出
最大值,并求出![]() 的最大值;
的最大值;
②求出使![]() 为直角三角形时
为直角三角形时![]() 的值;
的值;
(3)若抛物线上有且只有三个点![]() 到直线
到直线![]() 的距离是
的距离是![]() ,请直接写出此时由点
,请直接写出此时由点![]() ,
,![]() ,
,![]() ,
,![]() 构成的四边形的面积.
构成的四边形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com