
����Ŀ��̽���о�����֪����ABC�͡�CDE���ǵȱ������Σ�
��1����ͼ1������A��C��E��һ��ֱ����ʱ�����ǿ��Եõ����ۣ��߶�AD��BE��������ϵΪ���� �����߶�AD��BE���ɵ���Ƕ���Ϊ�� ���㣻
��2����ͼ2������A��C��E����һ��ֱ����ʱ����֤����1���еĽ�����Ȼ������
������ã�
��ͼ3��ij�㳡��һ���ı�������ABCD���ֲ�ã�AB��60m��BC��80m���ҡ�ABC��30�㣬��DAC����DCA��60�㣬����ˮ������B��D����֮��ľ��룮

���𰸡���1��AD=BE��60����2��֤������������3��ˮ������B��D����֮��ľ���Ϊ100m��
��������
������1�����ݵȱ������ε����ʿɵ�AC=BC��CD=CE����ACB=��DCE=60����Ȼ�������ACD=��BCE�����������߽DZ���֤����ACD����BCEȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�AD=BE������ȫ�������ζ�Ӧ����ȿɵá�ADC=��BEC��Ȼ����������ε�һ����ǵ������������ڵ������ڽǵĺ������DPE=��DCE����2��֤����ACD�ա�BCE��SAS�����õ�AD=BE����DAC=��EBC�����ݡ�BPA=180��-��ABP-��BAP=180��-��ABC-��BAC�����ɽ�𣮣�3����ͼ3����ABΪ������ABC������ȱ���ABE������CE���ɣ�2���ɵã�BD=CE��֤����EBC��ֱ�������Σ����ù��ɶ������CE�ij��ȣ����ɽ��
�����������1���ߡ�ABC����CDE���ǵȱ������Σ�
��AC=BC��CD=CE����ACB=��DCE=60�㣬
���ACB+��BCD=��DCE+��BCD������ACD=��BCE��
����ACD����BCE��
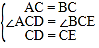 ��
��
���ACD�ա�BCE��SAS����
��AD=BE����ADC=��BEC��
�������ε�������ʣ���DPE=��PEA+��DAC����DCE=��ADC+��DAC��
���DPE=��DCE=60�㣻
�ʴ�Ϊ����ȣ�60��
��2���ߡ�ABC����CDE���ǵȱ������Σ�
��AC=BC��CD=CE����ACB=��DCE=60�㣬
���ACB+��BCD=��DCE+��BCD��
����ACD=��BCE��
����ACD����BCE��
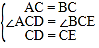 ��
��
���ACD�ա�BCE��SAS����
��AD=BE����DAC=��EBC��
���BPA=180�㩁��ABP����BAP=180�㩁��ABC����BAC=60��
��3����ͼ3����ABΪ������ABC������ȱ���ABE������CE��
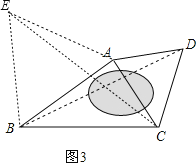
�ɣ�2���ɵã�BD=CE
���EBC=60��+30��=90�㣬
���EBC��ֱ��������
��EB=60m BC=80m��
��CE=![]() =100��m����
=100��m����
��ˮ������B��D����֮��ľ���Ϊ100m��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��PA����O��A��B���㣬AE�ǡ�O��ֱ������CΪ��O��һ�㣬��ACƽ�֡�PAE����C��CD��PA������ΪD��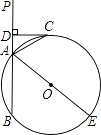
��1����֤��CDΪ��O�����ߣ�
��2����DC+DA=6����O��ֱ��Ϊ10����AB�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c����A��1��0����B��4��0����C��0��3�����㣮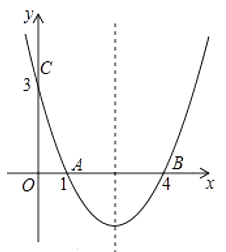
��1���������ߵĽ���ʽ��
��2���������ߵĶԳ������Ƿ���ڵ�P��ʹ���ı���PAOC���ܳ���С�������ڣ�����ı���PAOC�ܳ�����Сֵ���������ڣ���˵�����ɣ�
��3����ͼ�ڣ���Q���߶�OB��һ���㣬����BC�����߶�BC���Ƿ���������ĵ�M��ʹ��CQMΪ�����������ҡ�BQMΪֱ�������Σ������ڣ����M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
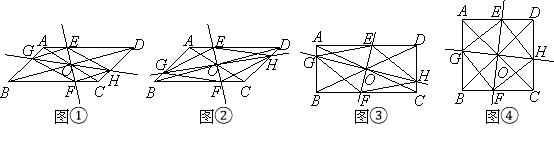
����Ŀ������������10������![]() ABCD�У�AC��BD���ڵ�O������O��ֱ��EF��GH���ֱ�ƽ���ı��ε���������E��G��F��H�ĵ㣬����EG��GF��FH��HE��
ABCD�У�AC��BD���ڵ�O������O��ֱ��EF��GH���ֱ�ƽ���ı��ε���������E��G��F��H�ĵ㣬����EG��GF��FH��HE��
��1����ͼ�������ж��ı���EGFH����״����˵��������
��2����ͼ������EF��GHʱ���ı���EGFH����״�� ��
��3����ͼ��������2���������£���AC=BD���ı���EGFH����״�� ��
��4����ͼ��������3���������£���AC��BD�����ж��ı���EGFH����״����˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�Ϊ(��1��0)��(3��0)����ͬʱ����A��B�ֱ�����ƽ��2����λ���ȣ�������ƽ��1����λ���ȣ��õ�A��B�Ķ�Ӧ��C��D������AC��BD��CD.
(1)ֱ��д����C��D�����꣬����ı���ABDC�������
(2)��x�����Ƿ����һ��F��ʹ��������DFC�������������DFB�����2���������ڣ��������F�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ����OABC����ֱ������ϵ�У�OΪ����ԭ�㣬��A��y���������ϣ���E�DZ�AB�ϵ�һ�����㣨�����A��B�غϣ�������E�ķ���������y= ![]() ��x��0����ͼ�����BC�����F��
��x��0����ͼ�����BC�����F��
��1������OAE����OCF������ֱ�ΪS1��S2 �� ��S1+S2=2����k��ֵ��
��2���ڣ�1���Ľ����£���OA=2��OC=4ʱ����������OEF�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У���E��BC����һ�㣬��BE��EC=2��1��AE��BD���ڵ�F�����AFD���ı���DFEC�����֮���� �� 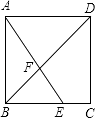
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һԪһ�β���ʽ��ʽ��
��1��3(x+2)-8��1-2(x-1)
��2��![]()
��3����ʽ��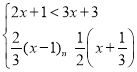 �ķǸ�������
�ķǸ�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com