练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

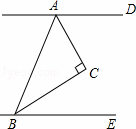
    如图，若AD∥BE，且∠ACB=90°，∠CBE=30°，则∠CAD=　　度．


    60            解：如图，延长AC交BE于F，

    ∵∠ACB=90°，∠CBE=30°，

    ∴∠1=90°﹣30°=60°，

    ∵AD∥BE，

    ∴∠CAD=∠1=60°．

    故答案为：60．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


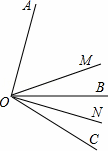
    如图，OM是∠AOC的平分线，ON是∠BOC的平分线．

    （1）当∠AOB=80°时，∠MON=　 　；

    （2）猜想∠MON与∠AOB有怎样的数量关系，写出结论并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    不等式组的解集是　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，∠A0B的两边0A，0B均为平面反光镜，∠A0B=40°．在射线0B上有一点P，从P点射出一束光线经0A上的Q点反射后，反射光线QR恰好与0B平行，则∠QPB的度数是（　　）

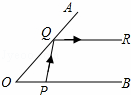
    A．  60°          B．80°          C．100°         D． 120°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知a，b，c为平面内三条不同直线，若a⊥b，c⊥b，则a与c的位置关系是　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    将一副三角板拼成如图所示的图形，过点C作CF平分∠DCE交DE于点F．

    （1）求证：CF∥AB；

    （2）求∠DFC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知AB∥CD，∠2=120°，则∠1的度数是（　　）

    A．  30°          B．60°          C．120°         D． 150°

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示，OA⊥OB，OC⊥OE，OD为∠BOC的平分线，∠BOE=16°，求∠DOE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


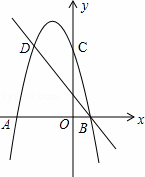
    如图，二次函数的图象与x轴交于A（﹣3，0）和B（1，0）两点，交y轴于点C（0，3），点C、D是二次函数图象上的一对对称点，一次函数的图象过点B、D．

    （1）请直接写出D点的坐标．

    （2）求二次函数的解析式．

    （3）根据图象直接写出使一次函数值大于二次函数值的x的取值范围．

    查看答案和解析>>

    同步练习册答案