
分析 先根据抛物线与x轴的交点求出A点和B点坐标,再利用配方法得到抛物线的顶点C的坐标,然后根据三角形面积公式求解即可.
解答 解:
当y=0时,-x2+3x+4=0,解得x1=4,x2=-1,
则A(4,0),B(-1,0),
所以AB=4-(-1)=5,
y=-x2+3x+4=-(x-1.5)2+6.25,则C(1.5,6.25),
所以△ABC的面积=$\frac{1}{2}$×5×6.25=15.625.
故答案为15.625.
点评 本题考查了抛物线与x轴的交点:利用二次函数的交点式:y=a(x-x1)(x-x2)(a,b,c是常数,a≠0)可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0),且这两个交点为抛物线上的对称点.


科目:初中数学 来源:2017届云南省普洱市九年级学业水平测试模拟考试(一)数学试卷(解析版) 题型:解答题
如图,菱形ABCD的对角线AC与BD相交于点O,且BE∥AC,CE∥BD.
(1)求证:四边形OBEC是矩形;
(2)若菱形ABCD的周长是 ,
,  ,求四边形OBEC的面积。
,求四边形OBEC的面积。

查看答案和解析>>
科目:初中数学 来源:2017届山东省日照市莒县第三协作区九年级3月学业水平模拟考试数学试卷(解析版) 题型:单选题
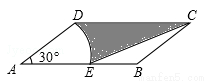
如图,在 ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是( )
ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是( )
A. 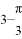 B.
B. 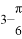 C.
C. 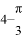 D.
D. 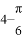
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
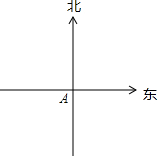 如图,一只渔船从岛A出发沿北偏东30°方向航行了50海里,遇到岛瞧(B点),又沿西北方向航行了25海里(此时记为C点).
如图,一只渔船从岛A出发沿北偏东30°方向航行了50海里,遇到岛瞧(B点),又沿西北方向航行了25海里(此时记为C点).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2017届山东省日照市莒县第三协作区九年级3月学业水平模拟考试数学试卷(解析版) 题型:单选题
如果关于x的一元二次方程kx2﹣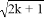 x+1=0有两个不相等的实数根,那么k的取值范围是( )
x+1=0有两个不相等的实数根,那么k的取值范围是( )
A. k< B. k<
B. k< 且k≠0 C. ﹣
且k≠0 C. ﹣ ≤k<
≤k< D. ﹣
D. ﹣ ≤k<
≤k< 且k≠0
且k≠0
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
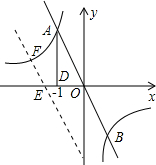 如图,反比例函数和正比例函数交于点A,B两点,A在第二象限,且点A的横坐标是-1,AD⊥x轴,垂足为D,△AOD的面积为1.
如图,反比例函数和正比例函数交于点A,B两点,A在第二象限,且点A的横坐标是-1,AD⊥x轴,垂足为D,△AOD的面积为1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com