
【题目】在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到AE,连结EC.如果AB=AC,∠BAC=90°.
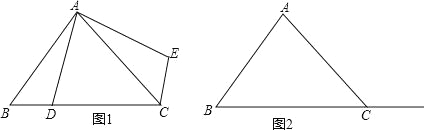
①当点D在线段BC上时(与点B不重合),如图1,请你判断线段CE、BD之间的位置和数量关系(直接写出结论);
②当点D在线段BC的延长线上时,请你在图2画出图形,判断①中的结论是否仍然成立,并证明你的判断.
【答案】(1)线段CE,BD之间的位置关系和数量关系为:CE=BD,CE⊥BD.(2)线段CE,BD之间的位置关系和数量关系为:CE=BD,CE⊥BD.
【解析】
试题分析:①线段AD绕点A逆时针旋转90°得到AE,根据旋转的性质得到AD=AE,∠BAD=∠CAE,得到△BAD≌△CAE,CE=BD,∠ACE=∠B,得到∠BCE=∠BCA+∠ACE=90°,于是有CE=BD,CE⊥BD.
②结论仍然成立.证明的方法与(1)类似.
试题解析:①结论:CE=BD,CE⊥BD.理由如下:
如图1中,∵AB=AC,∠BAC=90°,∴线段AD绕点A逆时针旋转90°得到AE,
∴AD=AE,∵∠BAC=∠DAE=90°,∴∠BAD=∠CAE,∵AB=AC,AD=AE,
∴△BAD≌△CAE,∴CE=BD,∠ACE=∠B,
∴∠BCE=∠BCA+∠ACE=90°,
∴线段CE,BD之间的位置关系和数量关系为:CE=BD,CE⊥BD.
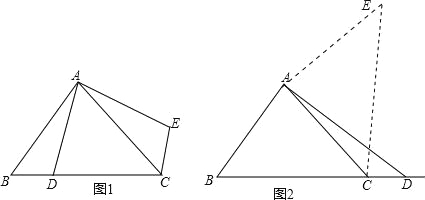
②结论仍然成立.理由如下:如图2中,∵线段AD绕点A逆时针旋转90°得到AE,
∴AE=AD,∠DAE=90°,∵AB=AC,∠BAC=90°,∴∠CAE=∠BAD,
∴△ACE≌△ABD,∴CE=BD,∠ACE=∠B,∴∠BCE=90°,
所以线段CE,BD之间的位置关系和数量关系为:CE=BD,CE⊥BD.


 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】“泥兴陶,,是钦州的一张文化名片。钦州市某妮兴陶公司以每只60元的价格销售一种成本价为40元的文化纪念杯,每星期可售出100只。后来经过市场调查发现,每只杯子的售价每降低1元,则平均何星期可多买出10只。若该公司销售这种文化纪念杯要想平均每星期获利2240元,请回答:
(1)每只杯应降价多少元?
(2)在平均每星期获利不变的情况下,为尽可能让利于顾客,赢得市场,该公司应该按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦期间,某宾馆有50个房间供游客居住,当每个房间每天的定价为180元时,房间会全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用.
(1)若房价定为200元时,求宾馆每天的利润;
(2)房价定为多少时,宾馆每天的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
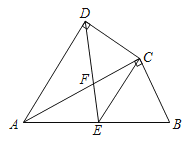
【题目】如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,AC交DE于点F.
(1)求证:AC2=ABAD;
(2)求证:CE∥AD;
(3)若AD=5,AB=6,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在解方程(x2﹣2x)2﹣2(x2﹣2x)-3=0时,设x2﹣2x=y,则原方程可转化为y2﹣2y-3=0,解得y1=-1,y2=3,所以x2﹣2x=-1或x2﹣2x=3,可得x1=x2=1,x3=3,x4=-1.我们把这种解方程的方法叫做换元法.对于方程:x2+![]() ﹣3x﹣
﹣3x﹣![]() =12,我们也可以类似用换元法设x+
=12,我们也可以类似用换元法设x+![]() =y,将原方程转化为一元二次方程,再进一步解得结果,那么换元得到的一元二次方程式是( )
=y,将原方程转化为一元二次方程,再进一步解得结果,那么换元得到的一元二次方程式是( )
A.y2﹣3y﹣12=0B.y2+y﹣8=0
C.y2﹣3y﹣14=0D.y2﹣3y﹣10=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1) 知识储备
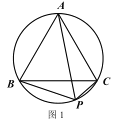
①如图 1,已知点 P 为等边△ABC 外接圆的弧BC 上任意一点.求证:PB+PC= PA.
②定义:在△ABC 所在平面上存在一点 P,使它到三角形三顶点的距离之和最小,则称点 P 为△ABC
的费马点,此时 PA+PB+PC 的值为△ABC 的费马距离.
(2)知识迁移
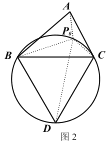
①我们有如下探寻△ABC (其中∠A,∠B,∠C 均小于 120°)的费马点和费马距离的方法:
如图 2,在△ABC 的外部以 BC 为边长作等边△BCD 及其外接圆,根据(1)的结论,易知线段____的长度即为△ABC 的费马距离.
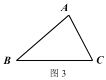
②在图 3 中,用不同于图 2 的方法作出△ABC 的费马点 P(要求尺规作图).
(3)知识应用
①判断题(正确的打√,错误的打×):
ⅰ.任意三角形的费马点有且只有一个(__________);
ⅱ.任意三角形的费马点一定在三角形的内部(__________).
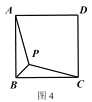
②已知正方形 ABCD,P 是正方形内部一点,且 PA+PB+PC 的最小值为![]() ,求正方形 ABCD 的
,求正方形 ABCD 的
边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm,点P由点B出发沿BA方向向点A匀速运动,同时点Q由点A出发沿AC方向向点C匀速运动,它们的速度均为lcm/s.连接PQ,设运动时间为t(s)(0<t<4).

(1)当t为何值时,PQ⊥AC?
(2)设△APQ的面积为S,求S与t的函数关系式,并求出当t为何值时,S取得最大值?S的最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
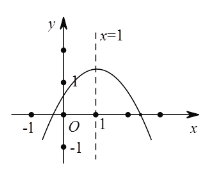
【题目】二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:①abc>0;②2a+b=0;③a-b+c>0;④当x≠1时,a+b>ax2+bx:⑤4ac<b2.其中正确的有____________(只填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com