
ЁОЬтФПЁП(1) жЊЪЖДЂБИ
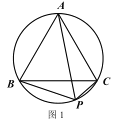
ЂйШчЭМ 1ЃЌвбжЊЕу P ЮЊЕШБпЁїABC ЭтНгдВЕФЛЁBC ЩЯШЮвтвЛЕуЃЎЧѓжЄЃКPB+PC= PA.
ЂкЖЈвхЃКдкЁїABC ЫљдкЦНУцЩЯДцдквЛЕу PЃЌЪЙЫќЕНШ§НЧаЮШ§ЖЅЕуЕФОрРыжЎКЭзюаЁЃЌдђГЦЕу P ЮЊЁїABC
ЕФЗбТэЕуЃЌДЫЪБ PA+PB+PC ЕФжЕЮЊЁїABC ЕФЗбТэОрРыЃЎ
(2)жЊЪЖЧЈвЦ
ЂйЮвУЧгаШчЯТЬНбАЁїABC (ЦфжаЁЯAЃЌЁЯBЃЌЁЯC ОљаЁгк 120Ёу)ЕФЗбТэЕуКЭЗбТэОрРыЕФЗНЗЈЃК
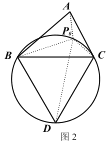
ШчЭМ 2ЃЌдкЁїABC ЕФЭтВПвд BC ЮЊБпГЄзїЕШБпЁїBCD МАЦфЭтНгдВЃЌИљОн(1)ЕФНсТлЃЌвзжЊЯпЖЮ____ЕФГЄЖШМДЮЊЁїABC ЕФЗбТэОрРы.
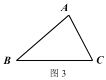
ЂкдкЭМ 3 жаЃЌгУВЛЭЌгкЭМ 2 ЕФЗНЗЈзїГіЁїABC ЕФЗбТэЕу P(вЊЧѓГпЙцзїЭМ).
(3)жЊЪЖгІгУ
ЂйХаЖЯЬтЃЈе§ШЗЕФДђЁЬЃЌДэЮѓЕФДђЁСЃЉЃК
ЂЁ.ШЮвтШ§НЧаЮЕФЗбТэЕугаЧвжЛгавЛИіЃЈ__________ЃЉЃЛ
ЂЂ.ШЮвтШ§НЧаЮЕФЗбТэЕувЛЖЈдкШ§НЧаЮЕФФкВПЃЈ__________ЃЉ.
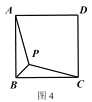
ЂквбжЊе§ЗНаЮ ABCDЃЌP ЪЧе§ЗНаЮФкВПвЛЕуЃЌЧв PA+PB+PC ЕФзюаЁжЕЮЊ![]() ЃЌЧѓе§ЗНаЮ ABCD ЕФ
ЃЌЧѓе§ЗНаЮ ABCD ЕФ
БпГЄЃЎ
ЁОД№АИЁП AD ЁЬ ЁС
ЁОНтЮіЁПЗжЮіЃКЃЈ1ЃЉИљОнвбжЊЪзЯШФмЕУЕНЁїPCEЮЊЕШБпШ§НЧаЮЃЌНјЖјЕУГіЁїACEЁеЁїBPCЃЌМДПЩЕУжЄЃЛ
ЃЈ2ЃЉЂйзаЯИдФЖСаТжЊЕФИХФюЃЌНсКЯЭМаЮЬиЕуЃЌжБНггаНсТлХаЖЯМДПЩЃЛ
ЂкИљОнГпЙцзїЭМЃЌзїЕШБпШ§НЧаЮМДПЩЧѓЕУЗбТэЕуЃЛ
ЃЈ3ЃЉЂйЂЁ.ИљОнзїЭМПЩжЊЗбТэЕугаЧвжЛгавЛИіЃЌЂЂ.гЩЭМ1КЭЭМ2ЃЌПЩжЊШЮвтШ§НЧаЮЕФЗбТэЕуВЛвЛЖЈЖМдкШ§НЧаЮЕФФкВПЃЛ
ЂкНЋЁїABPбиЕуBФцЪБеыа§зЊ60ЁуЕНЁїA1BP1ЃЌЙ§A1зїA1HЁЭBCЃЌНЛCBЕФбгГЄЯпгкHЃЌСЌНгP1PЃЌИљОнЕШБпШ§НЧаЮЕФХаЖЈгыаджЪЃЌЕУЕНЁїP1PBЪЧе§Ш§НЧаЮЃЌНјЖјЕУГіЁЯA1BH=30ЁуЃЌШЛКѓгЩе§ЗНаЮЕФаджЪКЭ30ЁуНЧжБНЧШ§НЧаЮЕФаджЪЃЌИљОнЙДЙЩЖЈРэЧѓГіе§ЗНаЮЕФБпГЄ.
ЯъНтЃКЃЈ1ЃЉЂйжЄУїЃКдкPAЩЯШЁвЛЕуEЃЌЪЙPE=PCЃЌСЌНгCEЃЌ
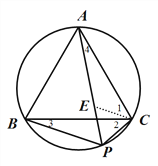
Ёпе§Ш§НЧаЮABC
ЁрЁЯAPC=ЁЯABC=60Ёу
гжЁпPE=PCЃЌЁрЁїPECЪЧе§Ш§НЧаЮ
ЁрCE=CP ЁЯACB=ЁЯECP=60Ёу
ЁрЁЯ1=ЁЯ2
гжЁпЁЯ3=ЁЯ4 BC=AC
ЁрЁїACEЁеЁїBCP (ASA)
ЁрAE=BP
МДЃКBP+CP=AP.
ЃЈ2ЃЉЂйЯпЖЮ AD ЕФГЄЖШМДЮЊЁїABCЕФЗбТэОрРыЃЎ
ЂкЙ§ABКЭACЗжБ№ЯђЭтзїЕШБпШ§НЧаЮЃЌСЌНгCDЃЌBEЃЌ
НЛЕуМДЮЊP0ЃЎ
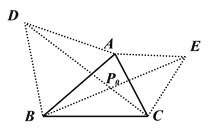
ЃЈ3ЃЉЂйЂЁ.ЃЈ ЁЬ ЃЉ ЂкЂЂ.ЃЈ ЁС ЃЉ
ЂкНтЃКНЋЁїABPбиЕуBФцЪБеыа§зЊ60ЁуЕНЁїA1BP1ЃЌ
Й§A1зїA1HЁЭBCЃЌНЛCBЕФбгГЄЯпгкHЃЌСЌНгP1PЃЌ
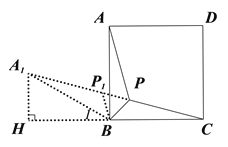
взЕУЃКA1B=ABЃЌPB=P1BЃЌPA=P1 A1ЃЌЁЯP1BP=ЁЯA1BA=60Ёу
ЁпPB=P1B ЁЯP1BP=60Ёу
ЁрЁїP1PBЪЧе§Ш§НЧаЮ
ЁрPP1=PB
ЁпPA+PB+PCЕФзюаЁжЕЮЊ![]()
ЁрP1A1+PP1+PCЕФзюаЁжЕЮЊ![]()
ЁрA1ЃЌP1ЃЌPЃЌCдкЭЌвЛжБЯпЩЯЃЌМДA1C=![]()
Щше§ЗНаЮЕФБпГЄЮЊ2x
ЁпЁЯA1BA=60Ёу ЁЯCBA=90Ёу
ЁрЁЯ1=30Ёу
дкRtЁїA1HBжаЃЌA1B=AB=2xЃЌЁЯ1=30Ёу
ЕУЃКA1H=xЃЌBH=![]()
дкRtЁїA1HCжаЃЌгЩЙДЙЩЖЈРэЕУЃК![]()
НтЕУЃКx1=1 x2=1ЃЈЩсШЅЃЉ
Ёре§ЗНаЮABCDЕФБпГЄЮЊ2ЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§yЃНЉxmЉ1+bxЉ3ЃЈmЃЌbЮЊГЃЪ§ЃЉЪЧЖўДЮКЏЪ§ЃЌЦфЭМЯѓЕФЖдГЦжсЮЊжБЯпxЃН1
ЃЈIЃЉЧѓИУЖўДЮКЏНЬЕФНтЮіЪНЃЛ
ЃЈЂђЃЉЕБЉ2ЁмxЁм0ЪБЃЌЧѓИУЖўДЮКЏЪ§ЕФКЏЪ§жЕyЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЬнаЮABCDжаЃЌABЁЮCDЃЌCEЦНЗжЁЯBCDЃЌCEЁЭADгкEЃЌDEЃН2AEЃЎШєЁїCEDУцЛ§ЮЊ1ЃЌдђЫФБпаЮABCEЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌЁЯACBЮЊШёНЧЃЎЕуDЮЊЩфЯпBCЩЯвЛЖЏЕуЃЌСЌНгADЃЌНЋЯпЖЮADШЦЕуAФцЪБеыа§зЊ90ЁуЕУЕНAEЃЌСЌНсECЃЎШчЙћAB=ACЃЌЁЯBAC=90ЁуЃЎ
ЂйЕБЕуDдкЯпЖЮBCЩЯЪБЃЈгыЕуBВЛжиКЯЃЉЃЌШчЭМ1ЃЌЧыФуХаЖЯЯпЖЮCEЁЂBDжЎМфЕФЮЛжУКЭЪ§СПЙиЯЕЃЈжБНгаДГіНсТлЃЉЃЛ
ЂкЕБЕуDдкЯпЖЮBCЕФбгГЄЯпЩЯЪБЃЌЧыФудкЭМ2ЛГіЭМаЮЃЌХаЖЯЂйжаЕФНсТлЪЧЗёШдШЛГЩСЂЃЌВЂжЄУїФуЕФХаЖЯЃЎ
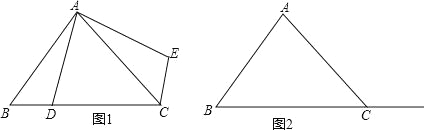
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЁїABCЕФШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊAЃЈЉ4ЃЌ3ЃЉЁЂBЃЈЉ3ЃЌ1ЃЉЁЂCЃЈЉ1ЃЌ3ЃЉЃЎ
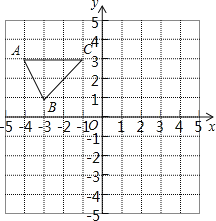
ЃЈ1ЃЉЧыАДЯТСавЊЧѓЛЭМЃК
ЂйНЋЁїABCЯШЯђгвЦНвЦ4ИіЕЅЮЛГЄЖШЁЂдйЯђЩЯЦНвЦ2ИіЕЅЮЛГЄЖШЃЌЕУЕНЁїA1B1C1ЃЌЛГіЁїA1B1C1ЃЛ
ЂкЁїA2B2C2гыЁїABCЙигкдЕуOГЩжааФЖдГЦЃЌЛГіЁїA2B2C2ЃЎ
ЃЈ2ЃЉдкЃЈ1ЃЉжаЫљЕУЕФЁїA1B1C1КЭЁїA2B2C2ЙигкЕуMГЩжааФЖдГЦЃЌЧыжБНгаДГіЖдГЦжааФMЕуЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАРЌЛјЗжРрЁБдНРДдНЪмЕНШЫУЧЕФЙизЂЃЌЮвЪаФГжабЇЖдВПЗжбЇЩњОЭЁАРЌЛјЗжРрЁБжЊЪЖЕФСЫНтГЬЖШЃЌВЩгУЫцЛњГщбљЕїВщЕФЗНЪНЃЌВЂИљОнЪеМЏЕНЕФаХЯЂНјааЭГМЦЃЌЛцжЦСЫЯТУцСНЗљЩаВЛЭъећЕФЭГМЦЭМЃЎИљОнЭМжааХЯЂЛиД№ЯТСаЮЪЬтЃК
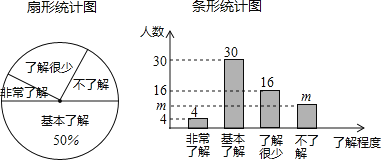
ЃЈ1ЃЉНгЪмЮЪОэЕїВщЕФбЇЩњЙВгаЁЁЁЁШЫЃЌЬѕаЮЭГМЦЭМжа![]() ЕФжЕЮЊЁЁЁЁЃЛ
ЕФжЕЮЊЁЁЁЁЃЛ
ЃЈ2ЃЉЩШаЮЭГМЦЭМжаЁАСЫНтКмЩйЁБВПЗжЫљЖдгІЩШаЮЕФдВаФНЧЕФЖШЪ§ЮЊЁЁЁЁЃЛ
ЃЈ3ЃЉШєДгЖдРЌЛјЗжРржЊЪЖДяЕНЁАЗЧГЃСЫНтЁБГЬЖШЕФ2УћФаЩњКЭ2УћХЎЩњжаЫцЛњГщШЁ2ШЫВЮМгРЌЛјЗжРржЊЪЖОКШќЃЌЧыгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЃЌЧѓЧЁКУГщЕН1УћФаЩњКЭ1УћХЎЩњЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
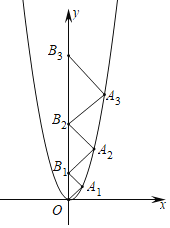
ЁОЬтФПЁПЖўДЮКЏЪ§yЃН2x2ЕФЭМЯѓШчЭМЫљЪОЃЌзјБъдЕуOЃЌЕуB1ЃЌB2ЃЌB3дкyжсЕФе§АыжсЩЯЃЌЕуA1ЃЌA2ЃЌA3дкЖўДЮКЏЪ§yЃН2x2ЮЛгкЕквЛЯѓЯоЕФЭМЯѓЩЯЃЌШєЁїA1OB1ЃЌЁїA2B1B2ЃЌЁїA3B2B3ЖМЮЊЕШбќжБНЧШ§НЧаЮЃЌЧвЕуA1ЃЌA2ЃЌA3ОљЮЊжБНЧЖЅЕуЃЌдђЕуA3ЕФзјБъЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєКЏЪ§yЃНaЃЈxЉhЃЉ2+kЃЈaЁй0ЃЉЕФЭМЯѓОЙ§дЕуЃЌзюДѓжЕЮЊ16ЃЌЧваЮзДгыХзЮяЯпyЃН4x2+2xЉ3ЯрЭЌЃЌдђДЫКЏЪ§ЕФЙиЯЕЪНЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊЛюдОСЊЛЖЭэЛсЕФЦјЗеЃЌзщжЏепЩшМЦСЫвдЯТзЊХЬгЮЯЗЃКAЁЂBСНИіДјжИеыЕФзЊХЬЗжБ№БЛЗжГЩШ§ИіУцЛ§ЯрЕШЕФЩШаЮЃЌзЊХЬAЩЯЕФЪ§зжЗжБ№ЪЧ1ЃЌ6ЃЌ8ЃЌзЊХЬBЩЯЕФЪ§зжЗжБ№ЪЧ4ЃЌ5ЃЌ7ЃЈСНИізЊХЬГ§БэУцЪ§зжВЛЭЌЭтЃЌЦфЫћЭъШЋЯрЭЌЃЉ.УПДЮбЁдё2УћЭЌбЇЗжБ№ВІЖЏAЁЂBСНИізЊХЬЩЯЕФжИеыЃЌЪЙжЎВњЩња§зЊЃЌжИеыЭЃжЙКѓЫљжИЪ§зжНЯДѓЕФвЛЗНЮЊЛёЪЄепЃЌИКепдђБэбнвЛИіНкФПЃЈШєМ§ЭЗЧЁКУЭЃСєдкЗжНчЯпЩЯЃЌдђжизЊвЛДЮЃЉ.зїЮЊгЮЯЗепЃЌФуЛсбЁдёAЁЂBжаФФИізЊХЬФиЃПВЂЧыЫЕУїРэгЩ.

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com