
����Ŀ�����������ࡱԽ��Խ�ܵ����ǵĹ�ע������ij��ѧ�Բ���ѧ���͡��������ࡱ֪ʶ���˽�̶ȣ����������������ķ�ʽ���������ռ�������Ϣ����ͳ�ƣ����������������в�������ͳ��ͼ������ͼ����Ϣ�ش��������⣺
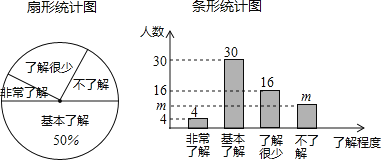
��1�������ʾ������ѧ�����������ˣ�����ͳ��ͼ��![]() ��ֵΪ������
��ֵΪ������
��2������ͳ��ͼ�С��˽���١���������Ӧ���ε�Բ�ĽǵĶ���Ϊ������
��3�����Ӷ���������֪ʶ�ﵽ���dz��˽⡱�̶ȵ�2��������2��Ů���������ȡ2�˲μ���������֪ʶ�����������б�����״ͼ�ķ�������ǡ�ó鵽1��������1��Ů���ĸ��ʣ�
���𰸡���1��60��10����2��96�㣻��3��![]()
��������
��1�����ݻ����˽����������ռ�İٷֱȿ������������m=������-�dz��˽������-�����˽������-�˽���ٵ�������
��2����������˽���١���ռ�������İٷֱȣ��ٳ���360�㼴�ɣ�
��3�������б�������״ͼ�ҵ����е�������ٴ����ҳ������1��������1��Ů������������ɸ��ʵ���������������������֮�������.
��1��![]()
![]()
��2�����˽���١���ռ�������İٷֱ�Ϊ![]()
�������Ե�Բ�ĽǵĶ���Ϊ![]()
��3��
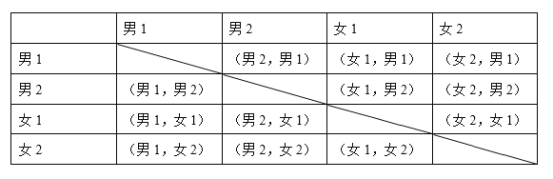
�ɱ����֪������12�ֽ��������1��������1��Ů������8�ֿ��ܣ�����ǡ�ó鵽1������1��Ů���ĸ���Ϊ![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y����x2+bx+c������C��0��3������x�ύ��A��B���㣬��A����1��0����
��I����������ߵĽ���ʽ��
������DΪ�����߶Գ�����һ�㣬����ACD���ܳ���Сʱ�����D�����ꣻ
�����������������Ƿ����һ��P��ʹCPǡ�ý���A��B��C��PΪ������ı��ε������Ϊ��ȵ������֣������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�У�ACƽ�֡�DAB����ADC����ACB��90����EΪAB���е㣬AC��DE�ڵ�F��
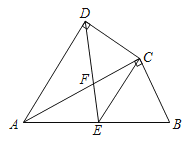
��1����֤��AC2��ABAD��
��2����֤��CE��AD��
��3����AD��5��AB��6����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڽⷽ�̣�x2��2x��2��2��x2��2x��-3��0ʱ����x2��2x=y����ԭ���̿�ת��Ϊy2��2y-3��0�����y1��-1��y2��3������x2��2x=-1��x2��2x=3���ɵ�x1=x2=1��x3=3��x4=-1.���ǰ����ֽⷽ�̵ķ���������Ԫ��.���ڷ��̣�x2+![]() ��3x��
��3x��![]() =12������Ҳ���������û�Ԫ����x+
=12������Ҳ���������û�Ԫ����x+![]() =y����ԭ����ת��ΪһԪ���η��̣��ٽ�һ����ý������ô��Ԫ�õ���һԪ���η���ʽ�ǣ� ��
=y����ԭ����ת��ΪһԪ���η��̣��ٽ�һ����ý������ô��Ԫ�õ���һԪ���η���ʽ�ǣ� ��
A.y2��3y��12��0B.y2+y��8��0
C.y2��3y��14��0D.y2��3y��10��0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1) ֪ʶ����
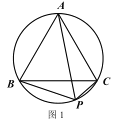
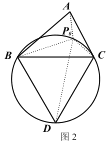
����ͼ 1����֪�� P Ϊ�ȱߡ�ABC ���Բ�Ļ�BC ������һ�㣮��֤��PB+PC= PA.
�ڶ��壺�ڡ�ABC ����ƽ���ϴ���һ�� P��ʹ����������������ľ���֮����С����Ƶ� P Ϊ��ABC
�ķ����㣬��ʱ PA+PB+PC ��ֵΪ��ABC �ķ������룮
(2)֪ʶǨ��
������������̽Ѱ��ABC (���С�A����B����C ��С�� 120��)�ķ�����ͷ�������ķ�����
��ͼ 2���ڡ�ABC ���ⲿ�� BC Ϊ�߳����ȱߡ�BCD �������Բ������(1)�Ľ��ۣ���֪�߶�____�ij��ȼ�Ϊ��ABC �ķ�������.
����ͼ 3 �У��ò�ͬ��ͼ 2 �ķ���������ABC �ķ����� P(Ҫ��߹���ͼ).
(3)֪ʶӦ��
���ж��⣨��ȷ�Ĵ�̣�����Ĵ������
��.���������εķ���������ֻ��һ����__________����
��.���������εķ�����һ���������ε��ڲ���__________��.
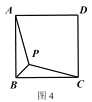
����֪������ ABCD��P ���������ڲ�һ�㣬�� PA+PB+PC ����СֵΪ![]() ���������� ABCD ��
���������� ABCD ��
�߳���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ó�̵��װ���������з��֣�����������ͯװƽ��ÿ������۳�20����ÿ��ӯ��40Ԫ��Ϊ��ӭ������һ����ͯ�ڣ��̳�������ȡ�ʵ��Ľ��۴�ʩ������������������ӯ����������ٿ�森�����鷢�֣�ÿ��ͯװÿ����1Ԫ���̳�ƽ��ÿ��ɶ�����2����
��1����ÿ��ͯװ����5Ԫ�����̳�ӯ������Ԫ��
��2�����̳�ÿ��Ҫ��ӯ��1200Ԫ����������̳���һ�㣬ÿ��ͯװӦ���۶���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
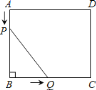
����Ŀ����ͼ��ʾ������ABC�У���ACB��90����AC��4cm��BC��3cm����P�ɵ�B������BA�������A�����˶���ͬʱ��Q�ɵ�A������AC�������C�����˶������ǵ��ٶȾ�Ϊlcm/s������PQ�����˶�ʱ��Ϊt��s����0��t��4����

��1����tΪ��ֵʱ��PQ��AC��
��2������APQ�����ΪS����S��t�ĺ�����ϵʽ���������tΪ��ֵʱ��Sȡ�����ֵ��S�����ֵ�Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڳ�����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() �ӵ�
�ӵ�![]() ��ʼ�ر�
��ʼ�ر�![]() ���յ�
���յ�![]() ��
��![]() ���ٶ��ƶ������ͬʱ����
���ٶ��ƶ������ͬʱ����![]() �ӵ�
�ӵ�![]() ��ʼ�ر�
��ʼ�ر�![]() ���յ�
���յ�![]() ��
��![]() ���ٶ��ƶ������
���ٶ��ƶ������![]() ��
��![]() �ֱ��
�ֱ��![]() ��
��![]() ͬʱ����������
ͬʱ����������![]() �˶�����
�˶�����![]() ʱ������ֹͣ�˶������˶�ʱ��Ϊ
ʱ������ֹͣ�˶������˶�ʱ��Ϊ![]() �룮
�룮
��1����գ�______��______��______��______���ú�t�Ĵ���ʽ��ʾ����
��2����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() �ij��ȵ���
�ij��ȵ���![]() ��
��
��3���Ƿ����![]() ���������
���������![]() �������ڣ��������ʱ
�������ڣ��������ʱ![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD��һ��E����BE��CE����C��CF��CE��BE�ӳ��߽��ڵ�F������DF��DE��CE��CF��1��DE��![]() �����н����У�����CBE�ա�CDF����BF��DF���۵�D��CF�ľ���Ϊ2����S�ı���DECF��
�����н����У�����CBE�ա�CDF����BF��DF���۵�D��CF�ľ���Ϊ2����S�ı���DECF��![]() +1��������ȷ���۵ĸ����ǣ�������
+1��������ȷ���۵ĸ����ǣ�������
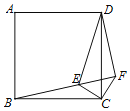
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com