
【题目】已知抛物线y=﹣x2+bx+c经过点C(0,3),与x轴交于A,B两点,点A(﹣1,0).
(I)求该抛物线的解析式;
(Ⅱ)D为抛物线对称轴上一点,当△ACD的周长最小时,求点D的坐标;
(Ⅲ)在抛物线上是否存在一点P,使CP恰好将以A,B,C,P为顶点的四边形的面积分为相等的两部分?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(I)y=﹣x2+2x+3;(Ⅱ)点D(1,2);(Ⅲ)点P(5,﹣12).
【解析】
(1)抛物线y=﹣x2+bx+c经过点C(0,3),则抛物线的表达式为:=﹣x2+bx+3,将点A的坐标代入上式,即可求解;
(2)抛物线的对称轴为:x=1,点A关于函数对称轴的对称点为点B(3,0),连接BC交抛物线的对称轴于点D,则点D为所求,即可求解;
(3)当点P在第一、二象限时,PC是四边形的边,故CP不可能平分以A,B,C,P为顶点的四边形的面积,当点P在第三、四象限时,设点P(m,﹣m2+2m+3),将点P、C的坐标代入一次函数表达式:y=sx+n并解得:
直线PC的表达式为:y=(2﹣m)x+3,过点A、B分别作CP的等距离的平行线m、n,分别交y轴于点M、N,则点C是MN的中点,即6=3m﹣6+2﹣m,即可求解.
解:(1)抛物线y=﹣x2+bx+c经过点C(0,3),则抛物线的表达式为:y═﹣x2+bx+3,
将点A的坐标代入上式并解得:b=2,
故抛物线的表达式为:y=﹣x2+2x+3;
(2)抛物线的对称轴为:x=1,点A关于函数对称轴的对称点为点B(3,0),
连接BC交抛物线的对称轴于点D,则点D为所求,
由点B、C的坐标得,直线BC的表达式为:y=﹣x+3,
当x=1时,y=2,
故点D(1,2);
(3)当点P在第一、二象限时,PC是四边形的边,故CP不可能平分以A,B,C,P为顶点的四边形的面积,
当点P在第三、四象限时,设点P(m,﹣m2+2m+3),
将点P、C的坐标代入一次函数表达式:y=sx+n并解得:
直线PC的表达式为:y=(2﹣m)x+3,
过点A、B分别作CP的等距离的平行线m、n,分别交y轴于点M、N,

则直线m的表达式为:y=(2﹣m)x+k,
将点A的坐标代入上式并解得:k=3m﹣6,即点M(0,3m﹣6),
同理可得:点N(0,2﹣m),
则点C是MN的中点,即6=3m﹣6+2﹣m,
解得:m=5,
故点P(5,﹣12).


科目:初中数学 来源: 题型:
【题目】在一次篮球比赛中,如图队员甲正在投篮.已知球出手时离地面![]() m,与篮圈中心的水平距离为7 m,球出手后水平距离为4 m时达到最大高度4 m,设篮球运行轨迹为抛物线,篮圈距地面3 m.
m,与篮圈中心的水平距离为7 m,球出手后水平距离为4 m时达到最大高度4 m,设篮球运行轨迹为抛物线,篮圈距地面3 m.
(1)建立如图所示的平面直角坐标系,问此球能否准确投中?
(2)此时,对方队员乙在甲面前1 m处跳起盖帽拦截,已知乙的最大摸高为3.1 m,那么他能否获得成功?

查看答案和解析>>
科目:初中数学 来源: 题型:
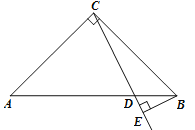
【题目】如图,已知Rt△ABC中,∠ACB=90°,AC=BC,D是线段AB上的一点(不与A、B重合).过点B作BE⊥CD,垂足为E.将线段CE绕点C顺时针旋转![]() ,得到线段CF,连结EF.设∠BCE度数为
,得到线段CF,连结EF.设∠BCE度数为![]() .
.
(1)①补全图形;
②试用含![]() 的代数式表示∠CDA.
的代数式表示∠CDA.
(2)若![]() ,求
,求![]() 的大小.
的大小.
(3)直接写出线段AB、BE、CF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果商场经销一种高档水果,原价每千克50元,连续两次降价后每千克32元,若每次下降的百分率相同.
(1)求每次下降的百分率;
(2)若每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,商场决定采取适当的涨价措施,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,且要尽快减少库存,那么每千克应涨价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=﹣xm﹣1+bx﹣3(m,b为常数)是二次函数,其图象的对称轴为直线x=1
(I)求该二次函教的解析式;
(Ⅱ)当﹣2≤x≤0时,求该二次函数的函数值y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
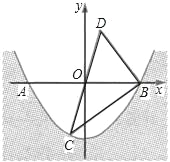
【题目】某水渠的横截面呈抛物线,水面的宽度为AB(单位:米),现以AB所在直线为x轴,以抛物线的对称轴为y轴建立如图所示的平面直角坐标系,设坐标原点为O.已知AB=8米,设抛物线解析式为y=ax2﹣4.
(1)求a的值;
(2)点C(﹣1,m)是抛物线上一点,点C关于原点O的对称点为点D,连接CD,BC,BD,求△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
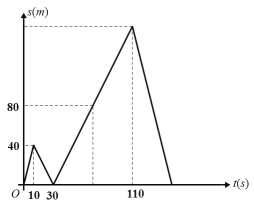
【题目】星期一升旗仪式前,李雷和韩梅梅两位数学课代表因为清 查作业耽搁了时间,打算匀速从教室跑到600 米外的中心广场 参加升旗仪式,出发时李雷发现鞋带松了,停下来系鞋带,韩 梅梅继续跑往中心广场,李雷系好鞋带后立即沿同一路线开始 追赶韩梅梅,李雷在途中追上韩梅梅后,担心迟到继续以原速 度往前跑,李雷到达操场时升旗仪式还没有开始,于是李雷站 在广场等待,韩梅梅继续跑往中心广场.设李雷和韩梅梅两人相距 s (米 ) ,韩梅梅跑步的时间为 t (秒), s 关于 t 的函数图象如图所示,则在整个运动过程 中,李雷和韩梅梅第一次相距 80 米后,再过_____秒钟两人再次相距 80 米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“垃圾分类”越来越受到人们的关注,我市某中学对部分学生就“垃圾分类”知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.根据图中信息回答下列问题:
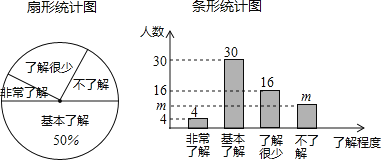
(1)接受问卷调查的学生共有 人,条形统计图中![]() 的值为 ;
的值为 ;
(2)扇形统计图中“了解很少”部分所对应扇形的圆心角的度数为 ;
(3)若从对垃圾分类知识达到“非常了解”程度的2名男生和2名女生中随机抽取2人参加垃圾分类知识竞赛,请用列表或画树状图的方法,求恰好抽到1名男生和1名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com