
【题目】二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:①abc>0;②2a+b=0;③a-b+c>0;④当x≠1时,a+b>ax2+bx:⑤4ac<b2.其中正确的有____________(只填序号).
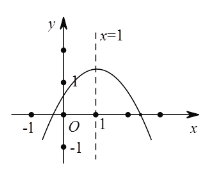
【答案】②④⑤
【解析】
先根据图象分析a、b、c的正负,再根据对称轴x=![]() 、与坐标轴的交点、顶点等情况分析,即可判断每一个选项的正确与否.
、与坐标轴的交点、顶点等情况分析,即可判断每一个选项的正确与否.
解:根据抛物线的开口方向可知a<0,它与y轴交点可知c>0,再根据对称轴x=![]() 在y轴右边,从而判断b>0,
在y轴右边,从而判断b>0,
∴abc<0,即答案①错误;
由图象可知抛物线对称轴是直线x=1,即x=![]() =1,b=-2a,
=1,b=-2a,
∴2a+b=0,即答案②正确;
由图象可知,当x=-1时,对应图象上的点在x轴下方,函数值小于0,
∴a-b+c<0,即答案③错误;
观察图象可知,当x=1时,函数取得最大值a+b+c,
∴当x≠1时,取得的函数值ax2+bx+c<a+b+c,即a+b>ax2+bx,答案④正确;
根据图象与x轴有两个不同交点可知,b2-4ac>0,
∴4ac<b2,即答案⑤正确.
故答案为:②④⑤.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
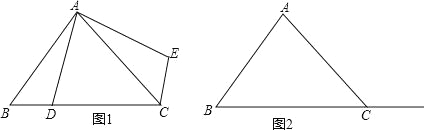
【题目】在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到AE,连结EC.如果AB=AC,∠BAC=90°.
①当点D在线段BC上时(与点B不重合),如图1,请你判断线段CE、BD之间的位置和数量关系(直接写出结论);
②当点D在线段BC的延长线上时,请你在图2画出图形,判断①中的结论是否仍然成立,并证明你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
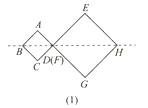
【题目】如图所示,四边形ABCD是边长为1的正方形,四边形EFGH是边长为2的正方形,点D与点F重合,点B、D(F)、H在同一条直线上.将正方形ABCD沿F→H方向平移到点B与点H重合时停止.设点D,F之间的距离为x,正方形ABCD与正方形EFGH重叠部分的面积为y,则能大致反映y与x之间函数关系的图像是( ).


A. 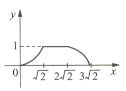 B.
B. 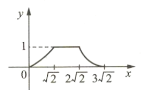 C.
C. 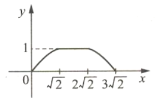 D.
D. 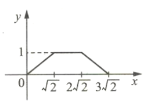
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图把一个长方形纸片沿EF 折叠后点D、C分别落在D′、C′的位置,若∠AED′=50°,则∠EFC =( ).
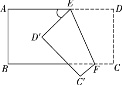
A.50°B.130°C.65°D.115°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A1B1C,连接AA1,若∠AA1B1=15°,则∠B的度数是( )

A. 75° B. 60° C. 50° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为活跃联欢晚会的气氛,组织者设计了以下转盘游戏:A、B两个带指针的转盘分别被分成三个面积相等的扇形,转盘A上的数字分别是1,6,8,转盘B上的数字分别是4,5,7(两个转盘除表面数字不同外,其他完全相同).每次选择2名同学分别拨动A、B两个转盘上的指针,使之产生旋转,指针停止后所指数字较大的一方为获胜者,负者则表演一个节目(若箭头恰好停留在分界线上,则重转一次).作为游戏者,你会选择A、B中哪个转盘呢?并请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
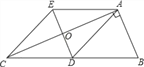
【题目】如图,在Rt△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连结EC.
(1)求证:AD=EC;
(2)求证:四边形ADCE是菱形;
(3)若AB=AO,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
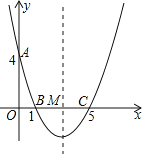
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com