
【题目】如图把一个长方形纸片沿EF 折叠后点D、C分别落在D′、C′的位置,若∠AED′=50°,则∠EFC =( ).
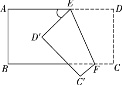
A.50°B.130°C.65°D.115°
科目:初中数学 来源: 题型:
【题目】如图,分别以△ABC的边AB,AC向两侧作等边三角形△ABD和△ACE,连接BE,CD.
(1)求证:BE=CD;
(2)△ADC可以看成 绕点A (填“顺时针”或“逆时针”)旋转了 °.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“慈善一日捐”活动中,为了解某校学生的捐款情况,抽样调查了该校部分学生的捐款数(单位:元),并绘制成下面的统计图.
(1)本次调查的样本容量是 ,这组数据的众数为 元;中位数为 元;
(2)求这组数据的平均数;
(3)该校共有600名学生参与捐款,请你估计该校学生的捐款总数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2﹣4x+c的图象经过坐标原点,与x轴交于点A(﹣4,0).

(1)求二次函数的解析式;
(2)在抛物线上存在点P,满足S△AOP=8,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:①abc>0;②2a+b=0;③a-b+c>0;④当x≠1时,a+b>ax2+bx:⑤4ac<b2.其中正确的有____________(只填序号).
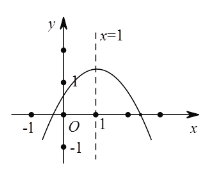
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知C(3,4),以点C为圆心的圆与y轴相切.点A、B在x轴上,且OA=OB.点P为⊙C上的动点,∠APB=90°,则AB长度的最大值为 _____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4
(a﹣b)(a4+a3b+a2b2+ab3+b4)=a5﹣b5
……
(1)根据规律可得(a﹣b)(an﹣1+an﹣2b+an﹣3b2+…+a2bn﹣3+abn﹣2+bn﹣1)= (其中n为正整数);
(2)仿照上面等式分解因式:a6﹣b6= ;
(3)根据规律可得(a﹣1)(an﹣1+an﹣2+…+a2+a+1)= (其中n为正整数);
(4)计算:(4﹣1)(410+49+48+…+42+4+1)= ;
(5)计算:(﹣2)2019+(﹣2)2018+(﹣2)2017+…+(﹣2)3+(﹣2)+1= .
查看答案和解析>>
科目:初中数学 来源: 题型:
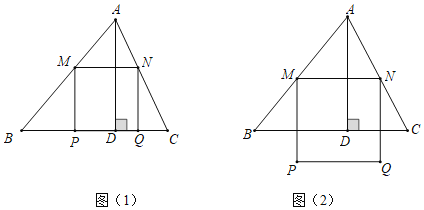
【题目】如图在锐角△ABC中,BC=6,高AD=4,两动点M、N分别在AB、AC上滑动(不包含端点),且MN∥BC,以MN为边长向下作正方形MPQN,设MN=x,正方形MPQN与△ABC公共部分的面积为y.
(1)如图(1),当正方形MPQN的边P恰好落在BC边上时,求x的值;
(2)如图(2),当PQ落△ABC外部时,求出y与x的函数关系式(写出x的取值范围)并求出x为何值时y最大,最大是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com