
【题目】如图,在平面直角坐标系中,已知C(3,4),以点C为圆心的圆与y轴相切.点A、B在x轴上,且OA=OB.点P为⊙C上的动点,∠APB=90°,则AB长度的最大值为 _____.

科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣4,3)、B(﹣3,1)、C(﹣1,3).
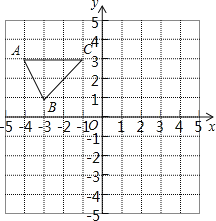
(1)请按下列要求画图:
①将△ABC先向右平移4个单位长度、再向上平移2个单位长度,得到△A1B1C1,画出△A1B1C1;
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2.
(2)在(1)中所得的△A1B1C1和△A2B2C2关于点M成中心对称,请直接写出对称中心M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铜陵市义安区实施了城乡居民基本医疗保险(简称“医疗保险”),办法规定农村村民只要每人每年交纳180元钱就可以加入医疗保险,住院时自己先垫付,出院同时就可得到按一定比例的报销款,这项举措惠及民生,吴斌与同学随机调查了他们镇的一些农民,根据收集到的数据绘制了以下的统计图.
根据图中信息,解答下列问题:
(1)本次调查了多少村民?被调查的村民中参加医疗保险,得到报销款的有多少人?
(2)若该镇有34000村民,请估算有多少人参加了医疗保险?要使两年后参加医疗保险的人数增加到业务31460人,假设这两年的年增长率相同,求年增长率?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图把一个长方形纸片沿EF 折叠后点D、C分别落在D′、C′的位置,若∠AED′=50°,则∠EFC =( ).
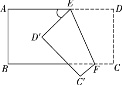
A.50°B.130°C.65°D.115°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]()
![]() 对称轴为______,顶点坐标为______;
对称轴为______,顶点坐标为______;
![]() 在坐标系中利用五点法画出此抛物线.
在坐标系中利用五点法画出此抛物线.
x |
| ______ | ______ | ______ | ______ | ______ |
|
y |
| ______ | ______ | ______ | ______ | ______ |
|
![]() 若抛物线与x轴交点为A、B,点
若抛物线与x轴交点为A、B,点![]() 在抛物线上,求
在抛物线上,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为活跃联欢晚会的气氛,组织者设计了以下转盘游戏:A、B两个带指针的转盘分别被分成三个面积相等的扇形,转盘A上的数字分别是1,6,8,转盘B上的数字分别是4,5,7(两个转盘除表面数字不同外,其他完全相同).每次选择2名同学分别拨动A、B两个转盘上的指针,使之产生旋转,指针停止后所指数字较大的一方为获胜者,负者则表演一个节目(若箭头恰好停留在分界线上,则重转一次).作为游戏者,你会选择A、B中哪个转盘呢?并请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:为解方程(x2﹣1)2﹣5(x2﹣1)+4=0,我们可以将x2﹣1视为一个整体,然后设x2﹣1=y,则(x2﹣1)2=y2,原方程化为y2﹣5y+4=0.
解得y1=1,y2=4
当y=1时,x2﹣1=1.∴x2=2.∴x=±![]() ;
;
当y=4时,x2﹣1=4,∴x2=5,∴x=±![]() .
.
∴原方程的解为x1=![]() ,x2=﹣
,x2=﹣![]() ,x3=
,x3=![]() ,x4=﹣
,x4=﹣![]() ,
,
请利用以上知识解决下列问题:
如果(m2+n2﹣1)(m2+n2+2)=4,则m2+n2=__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江苏是全国首个自然村“村村通宽带”省份.我市某村为了将当地农产品外销,建立了淘宝网店.该网店于今年7月底以每袋25元的成本价收购一批农产品.当商品售价为每袋40元时,8月份销售256袋.9、10月该商品十分畅销.销售量持续走高.在售价不变的基础上,10月份的销售量达到400袋.设9、10这两个月月平均增长率不变.
(1)求9、10这两个月的月平均增长率;
(2)为迎接双“十一”,11月份起,该网店采用降价促销的方式回馈顾客,经调查发现,该农产品每降价1元/每袋,销售量就增加5袋,当农产品每袋降价多少元时,该淘宝网店11月份获利4250元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上一点,
上一点,![]() ,连接
,连接![]() .
.
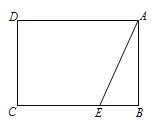
(1)沿![]() 翻折
翻折![]() 使点
使点![]() 落在点
落在点![]() 处,
处,
①连接![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
②连接![]() ,若
,若![]() ,求
,求![]() 的取值范围.
的取值范围.
(2)![]() 绕点
绕点![]() 顺时针旋转得
顺时针旋转得![]() ,点
,点![]() 落在边
落在边![]() 上时旋转停止. 若点
上时旋转停止. 若点![]() 落在矩形对角线
落在矩形对角线![]() 上,且点
上,且点![]() 到
到![]() 的距离小于
的距离小于![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com