
【题目】如图,二次函数y=ax2﹣4x+c的图象经过坐标原点,与x轴交于点A(﹣4,0).

(1)求二次函数的解析式;
(2)在抛物线上存在点P,满足S△AOP=8,请直接写出点P的坐标.
【答案】(1)y=-![]() -4x P1(-2, 4),P2(-2+2
-4x P1(-2, 4),P2(-2+2![]() ,-4),P3(-2-2
,-4),P3(-2-2![]() ,-4)
,-4)
【解析】试题分析:(1)把点A原点的坐标代入函数解析式,利用待定系数法求二次函数解析式解答;
(2)根据三角形的面积公式求出点P到AO的距离,然后分点P在x轴的上方与下方两种情况解答即可.
试题解析:(1)由已知条件得![]() ,
,
解得![]() ,
,
所以,此二次函数的解析式为y=﹣x2﹣4x;
(2)∵点A的坐标为(﹣4,0),
∴AO=4,
设点P到x轴的距离为h,
则S△AOP=![]() ×4h=8,
×4h=8,
解得h=4,
①当点P在x轴上方时,﹣x2﹣4x=4,
解得x=﹣2,
所以,点P的坐标为(﹣2,4),
②当点P在x轴下方时,﹣x2﹣4x=﹣4,
解得x1=﹣2+2![]() ,x2=﹣2﹣2
,x2=﹣2﹣2![]() ,
,
所以,点P的坐标为(﹣2+2![]() ,﹣4)或(﹣2﹣2
,﹣4)或(﹣2﹣2![]() ,﹣4),
,﹣4),
综上所述,点P的坐标是:(﹣2,4)、(﹣2+2![]() ,﹣4)、(﹣2﹣2
,﹣4)、(﹣2﹣2![]() ,﹣4).
,﹣4).


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】已知△ABC为等腰直角三角形,∠ACB=90°,点A在直线DE上,过C点作CF⊥DE于F,过B点作BG⊥DE于G.
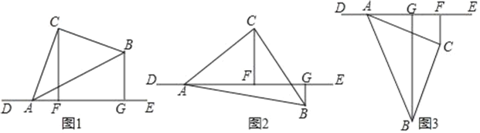
(1)发现问题:如图1,当B、C两点均在直线DE上方时,线段AG、BG和CF存在的数量关系是 .
(2)类比探究:当△ABC绕点A顺时针旋转至图2的位置时,线段AG、BG和CF之间的数量关系是否会发生变化?如果不变,请说明理由;如果变化,请写出你的猜想,并给予证明;
(3)拓展延伸:当△ABC绕点A顺时针旋转至图3的位置时,若CF=1,AG=2,请直接写出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.
如图所示,底座上A,B两点间的距离为90cm.低杠上点C到直线AB的距离CE的长为155cm,高杠上点D到直线AB的距离DF的长为234cm,已知低杠的支架AC与直线AB的夹角∠CAE为82.4°,高杠的支架BD与直线AB的夹角∠DBF为80.3°.求高、低杠间的水平距离CH的长.(结果精确到1cm,参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.983,cos80.3°≈0.168,tan80.3°≈5.850)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(2,0).OC=3OB.
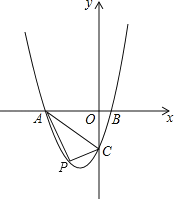
(1)求抛物线的解析式;
(2)若点P是线段AC下方抛物线上的动点,求三角形PAC面积的最大值.
(3)在(2)的条件下,△PAC的面积为S,其中S为整数的点P作“好点”,则存在多个“好点”,则所有“好点”的个数为
(4)在(2)的条件下,以PA为边向直线AC右上侧作正方形APHG,随着点P的运动,正方形的大小、位置也随之改变,当顶点H或G恰好落在y轴上时,直接写出对应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节那天,小贤回家看到桌上有一盘粽子,其中有豆沙粽、肉粽各1个,蜜枣粽2个,这些粽子除馅外无其他差别.
(1)小贤随机地从盘中取出一个粽子,取出的是肉粽的概率是多少?
(2)小贤随机地从盘中取出两个粽子,试用画树状图或列表的方法表示所有可能的结果,并求出小贤取出蜜枣粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是等腰Rt△ABC外一点,把线段BP绕点B顺时针旋转90°得到线段BP',已知∠AP'B=135°,P'A:P'C=1:3,则P'A:PB=_____.
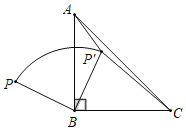
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC垂足为E.
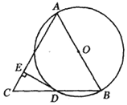
(1)求证:AB=AC;
(2)若⊙O半径为5,∠BAC=60°,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
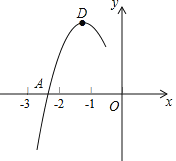
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确结论是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把抛物线![]() 先向左平移
先向左平移![]() 个单位长度,再向上平移
个单位长度,再向上平移![]() 个单位长度,得到抛物线
个单位长度,得到抛物线![]() .
.
(1)试确定![]() 的值;
的值;
(2)作原抛物线关于![]() 轴对称的图形,求所得抛物线的函数表达式.
轴对称的图形,求所得抛物线的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com