
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC垂足为E.
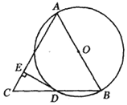
(1)求证:AB=AC;
(2)若⊙O半径为5,∠BAC=60°,求DE的长.
 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
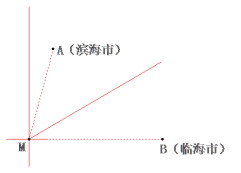
【题目】如图,在海面上生成了一股强台风,台风中心(记为点M)位于滨海市(记作点A)的南偏西15°,距离为![]() 千米,且位于临海市(记作点B)正西方向
千米,且位于临海市(记作点B)正西方向![]() 千米处.台风中心正以72千米/时的速度沿北偏东60°的方向移动(假设台风在移动过程中的风力保持不变),距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.
千米处.台风中心正以72千米/时的速度沿北偏东60°的方向移动(假设台风在移动过程中的风力保持不变),距离台风中心60千米的圆形区域内均会受到此次强台风的侵袭.
(1)滨海市、临海市是否会受到此次台风的侵袭?请说明理由.
(2)若受到此次台风侵袭,该城市受到台风侵袭的持续时间有多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2﹣4x+c的图象经过坐标原点,与x轴交于点A(﹣4,0).

(1)求二次函数的解析式;
(2)在抛物线上存在点P,满足S△AOP=8,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
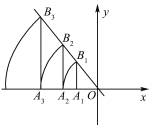
【题目】如图,直线l:y=-![]() x,点A1的坐标为(-3,0). 过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…按此做法进行下去,点A2 017的坐标为 ( )
x,点A1的坐标为(-3,0). 过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…按此做法进行下去,点A2 017的坐标为 ( )
A.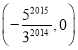 B.
B.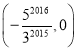 C.
C.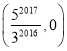 D.
D.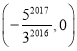
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的对角线AC与BD相交于点O.将∠COB绕点O顺时针旋转,设旋转角为α(0<α<90°),角的两边分别与BC,AB交于点M,N,连接DM,CN,MN,下列四个结论:①∠CDM=∠COM;②CN⊥DM;③△CNB≌△DMC;④AN2+CM2=MN2;其中正确结论的个数是( )

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1 ,它与x轴交于两点O,A;将C1绕点A旋转180°得到C2 , 交x轴于A1;将C2绕点A1旋转180°得到C3 , 交x轴于点A2 . .....如此进行下去,直至得到C2018 , 若点P(4035,m)在第2018段抛物线上,则m的值为________.
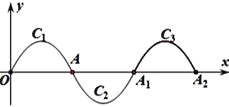
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
(1)请直接写出D点的坐标.
(2)求二次函数的解析式.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在的圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com