
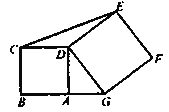
【题目】如图,A在线段BG上,ABCD和DEFG都是正方形,面积分别为7和11,则△CDE的面积等于 .
【答案】![]()
【解析】
过E点和G点分别作△CDE和△DGF的高CP和GH,证明△DCP与△DGH全等,得出CP=DH,再根据勾股定理求出DH=AG,通过求三角形的面积可得到答案.
过E点和G点分别作△CDE和△DGF的高CP和GH,
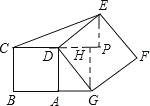
∵DGFC是正方形,
∴DG=DE,∠EDG=90°,
∵∠EDP+∠HDG=90°
∵∠EDP+∠DEP=90°,
∴∠HDG=∠DEP,
在△EDP与△DGH中,
∴△EDP≌△DGH(AAS),
∴DH=PE,
∵∠DAG=∠DHG=90°,∠ADH=∠AGH=90°
∴四边形ADHG是矩形,
∴AG=DH,
∵正方形ABCD和正方形DEFG的面积分别为7和11,
∴CD=AD=![]() ,DG=
,DG=![]() ,
,
在Rt△ADG中,
AG=![]() ,
,
∴PE=2,
∴△CDE的面积=![]() CDPE=
CDPE=![]() ×
×![]() ×2=
×2=![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】我们知道:任何有理数的平方都是一个非负数,即对于任何有理数a,都有a2≥0成立,所以,当a=0时,a2有最小值0.
(应用):(1)代数式(x-1)2有最小值时,x=___1;
(2)代数式m2+3的最小值是____3;
(探究):求代数式n2+4n+9的最小值,小明是这样做的:
n2+4n+9
=n2+4n+4+5
=(n+2)2+5
∴当n=-2时,代数式n2+4n+9有最小值,最小值为5.
请你参照小明的方法,求代数式a2-6a-3的最小值,并求此时a的值.
(拓展):(3)代数式m2+n2-8m+2n+17=0,求m+n的值.
(4)若y=-4t2+12t+6,直接写出y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
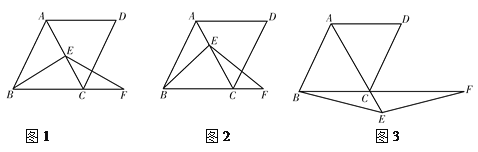
(1)如图1,当E是线段AC的中点,且AB=2时,求△ABC的面积;
(2)如图2,当点E不是线段AC的中点时,求证:BE=EF;
(3)如图3,当点E是线段AC延长线上的任意一点时,(2)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“高低杠”是女子体操特有的一个竞技项目,其比赛器材由高、低两根平行杠及若干支架组成,运动员可根据自己的身高和习惯在规定范围内调节高、低两杠间的距离.某兴趣小组根据高低杠器材的一种截面图编制了如下数学问题,请你解答.
如图所示,底座上A,B两点间的距离为90cm.低杠上点C到直线AB的距离CE的长为155cm,高杠上点D到直线AB的距离DF的长为234cm,已知低杠的支架AC与直线AB的夹角∠CAE为82.4°,高杠的支架BD与直线AB的夹角∠DBF为80.3°.求高、低杠间的水平距离CH的长.(结果精确到1cm,参考数据sin82.4°≈0.991,cos82.4°≈0.132,tan82.4°≈7.500,sin80.3°≈0.983,cos80.3°≈0.168,tan80.3°≈5.850)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.
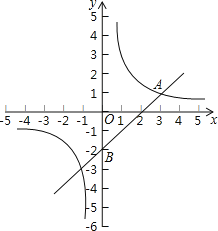
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(2,0).OC=3OB.
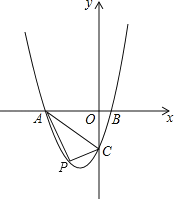
(1)求抛物线的解析式;
(2)若点P是线段AC下方抛物线上的动点,求三角形PAC面积的最大值.
(3)在(2)的条件下,△PAC的面积为S,其中S为整数的点P作“好点”,则存在多个“好点”,则所有“好点”的个数为
(4)在(2)的条件下,以PA为边向直线AC右上侧作正方形APHG,随着点P的运动,正方形的大小、位置也随之改变,当顶点H或G恰好落在y轴上时,直接写出对应的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节那天,小贤回家看到桌上有一盘粽子,其中有豆沙粽、肉粽各1个,蜜枣粽2个,这些粽子除馅外无其他差别.
(1)小贤随机地从盘中取出一个粽子,取出的是肉粽的概率是多少?
(2)小贤随机地从盘中取出两个粽子,试用画树状图或列表的方法表示所有可能的结果,并求出小贤取出蜜枣粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连结AC,过点D作DE⊥AC垂足为E.
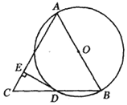
(1)求证:AB=AC;
(2)若⊙O半径为5,∠BAC=60°,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
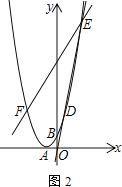
【题目】已知抛物线顶点![]() 在
在![]() 轴负半轴上,与
轴负半轴上,与![]() 轴交于点
轴交于点![]() ,
,![]() ,
,![]() 为等腰直角三角形.
为等腰直角三角形.
(1)求抛物线的解析式
(2)若点![]() 在抛物线上,若
在抛物线上,若![]() 为直角三角形,求点
为直角三角形,求点![]() 的坐标
的坐标
(3)已知直线![]() 过点
过点![]() ,交抛物线于点
,交抛物线于点![]() 、
、![]() ,过
,过![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,求证:直线
,求证:直线![]() 经过一个定点,并求定点的坐标.
经过一个定点,并求定点的坐标.
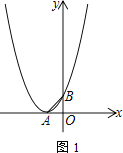
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com