
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.
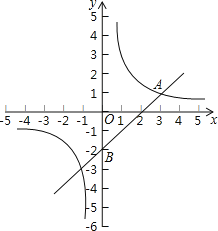
【答案】(1)y=![]() ;y=x-2;(2)(0,0)或(4,0)
;y=x-2;(2)(0,0)或(4,0)
【解析】试题分析:(1)利用待定系数法即可求得函数的解析式;
(2)首先求得AB与x轴的交点,设交点是C,然后根据S△ABP=S△ACP+S△BCP即可列方程求得P的横坐标.
试题解析:(1)∵反比例函数y=![]() (m≠0)的图象过点A(3,1),
(m≠0)的图象过点A(3,1),
∴3=![]()
∴m=3.
∴反比例函数的表达式为y=![]() .
.
∵一次函数y=kx+b的图象过点A(3,1)和B(0,-2).
∴![]() ,
,
解得: ![]() ,
,
∴一次函数的表达式为y=x-2;
(2)令y=0,∴x-2=0,x=2,
∴一次函数y=x-2的图象与x轴的交点C的坐标为(2,0).
∵S△ABP=3,
![]() PC×1+
PC×1+![]() PC×2=3.
PC×2=3.
∴PC=2,
∴点P的坐标为(0,0)、(4,0).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
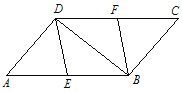
【题目】如图,在□ABCD 中,∠ADB=90°,点 E 为 AB 边的中点,点 F 为CD 边的中点.
(1)求证:四边形 DEBF 是菱形;
(2)当∠A 等于多少度时,四边形 DEBF 是正方形?并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对全校1200名学生进行“校园安全知识”的教育活动,从1200名学生中随机抽取部分学生进行测试,成绩评定按从高分到低分排列分为![]() ,
, ![]() ,
, ![]() ,
, ![]() 四个等级,绘制了图①、图②两幅不完整的统计图.请结合图中所给信息解答下列问题:
四个等级,绘制了图①、图②两幅不完整的统计图.请结合图中所给信息解答下列问题:
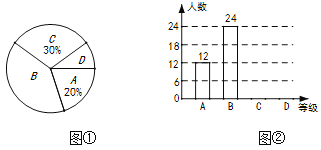
(1)求本次被抽查的学生共有多少名?
(2)将条形统计图和扇形统计图补充完整;
(3)求扇形统计图中“![]() ”所在的扇形圆心角的度数;
”所在的扇形圆心角的度数;
(4)估计全校“![]() ”等级的学生有多少名?
”等级的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
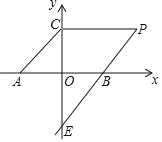
【题目】如图,直线y=x+3与x轴、y轴分别相交于A、C两点,过点B(6,0),E(0,﹣6)的直线上有一点P,满足∠PCA=135°.
(1)求证:四边形ACPB是平行四边形;
(2)求直线BE的解析式及点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪在复习过程中,发现数轴上线段的长度可以用线段端点表示的数进行减法运算得到,例:
如图1,线段![]() ,线段
,线段![]() ,
,

线段![]() ,线段
,线段![]()
结论:数轴上任意两点表示的数分别为:![]() ,
,![]() (
(![]() ),则这两点间的距离为:
),则这两点间的距离为:![]() (即:较大的数减去较小的数).
(即:较大的数减去较小的数).
尝试应用:
(1)若数轴上点![]() ,点
,点![]() 代表的数分别是-3,-1,则
代表的数分别是-3,-1,则![]() ______.
______.
(2)把一条数轴在数![]() 处对折,表示-9和3两数的点恰好互相重合,此时
处对折,表示-9和3两数的点恰好互相重合,此时![]() ______.
______.
(3)数轴上的两个点之间的距离为6,其中一个点表示的数为3,另一个点表示的数为![]() ,则
,则![]() ______.
______.
问题解决:
(4)如图2,点![]() 表示数
表示数![]() ,点
,点![]() 表示-2,点
表示-2,点![]() 表示
表示![]() 且
且![]() ,问点
,问点![]() 和点
和点![]() 分别表示什么数?为什么?
分别表示什么数?为什么?

(5)上述(4)的条件下,图2所示的数轴上,是否存在满足条件的点![]() ,使用
,使用![]() ?
?
若存在,请直接写出![]() 所表示的数,若不存在,请说明理由?(点
所表示的数,若不存在,请说明理由?(点![]() 不与点
不与点![]() ,点
,点![]() ,点
,点![]() 重合)
重合)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知代数式![]() ,当
,当![]() 时,该代数式的值为3.
时,该代数式的值为3.
(1)求c的值;
(2)已知:当![]() 时,该代数式的值为0.
时,该代数式的值为0.
①求:当![]() 时,该代数式的值;
时,该代数式的值;
②若![]() ,
,![]() ,
,![]() ,试比较a与d的大小,并说明理由.
,试比较a与d的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )
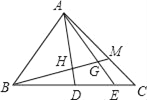
A. 3:2:1 B. 5:3:1 C. 25:12:5 D. 51:24:10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人民生活水平的提高,汽车进入家庭的越来越多.我市某小区在2007年底拥有家庭轿车64辆,到了2009年底,家庭轿车数为100辆.
(1)若平均每年轿车数的增长率相同,求这个增长率.
(2)为了缓解停车矛盾,多增加一些车位,该小区决定投资15万元,再造一些停车位.据测算,建造一个室内停车位,需5000元;建造一个室外停车位,需1000元.按实际情况考虑,计划室外停车位数不少于室内车位的2倍,又不能超过室内车位的2.5倍.问,该小区有哪几种建造方案?应选择哪种方案最合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
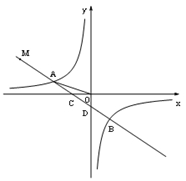
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() 两点,与
两点,与![]() 轴、
轴、![]() 轴分别交于C、D两点.已知:
轴分别交于C、D两点.已知: ![]() ,点B的坐标为
,点B的坐标为![]() .
.
(1)求该反比例函数的解析式和点D的坐标;
(2)点M在射线CA上,且MA=2AC,求△MOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com