
【题目】某中学对全校1200名学生进行“校园安全知识”的教育活动,从1200名学生中随机抽取部分学生进行测试,成绩评定按从高分到低分排列分为![]() ,
, ![]() ,
, ![]() ,
, ![]() 四个等级,绘制了图①、图②两幅不完整的统计图.请结合图中所给信息解答下列问题:
四个等级,绘制了图①、图②两幅不完整的统计图.请结合图中所给信息解答下列问题:
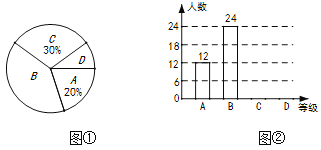
(1)求本次被抽查的学生共有多少名?
(2)将条形统计图和扇形统计图补充完整;
(3)求扇形统计图中“![]() ”所在的扇形圆心角的度数;
”所在的扇形圆心角的度数;
(4)估计全校“![]() ”等级的学生有多少名?
”等级的学生有多少名?
【答案】(1)本次被抽查的学生共有60名;
(2)补充完整条形统计图和扇形统计图见解析;
(3)扇形统计图中“![]() ”所在的扇形圆心角的度数;
”所在的扇形圆心角的度数;
(4)估计全校“![]() ”等级的学生有120名.
”等级的学生有120名.
【解析】分析:(1)根据A等级有12人,占20%,即可求得抽查的总人数;
(2)根据百分比的定义求得B、D所占的百分比,以及C、D类的人数,即可解答;
(3)利用360°乘以对应的百分比即可求解;(4)利用总人数1200乘以对应的百分比.
本题解析:(1)12÷20%=60(名);
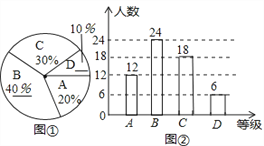
(2)B所占的百分比是: ![]() ×100%=40%,
×100%=40%,
D所占的百分比是:
1﹣20%﹣40%﹣30%=10%.
C的个数是:60×30%=18(名),
D的个数是:60×10%=6(名).
(3)360°×20%=72°;
(4)1200×10%=120(名).
答:估计全校“D”等级的学生有120(名).


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
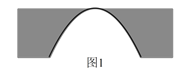
【题目】河上有一座桥孔为抛物线形的拱桥(如图 ![]() ),水面宽
),水面宽 ![]() 时,水面离桥孔顶部
时,水面离桥孔顶部 ![]() ,因降暴雨水面上升
,因降暴雨水面上升 ![]() .
.
(1)建立适当的坐标系,并求暴雨后水面的宽;(结果保留根号)
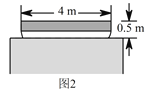
(2)一艘装满物资的小船,露出水面的部分高为 ![]() ,宽
,宽 ![]() (横断面如图
(横断面如图 ![]() 所示),暴雨后这艘船能从这座拱桥下通过吗?
所示),暴雨后这艘船能从这座拱桥下通过吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
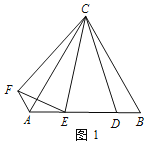
【题目】【操作发现】如图 1,△ABC 为等边三角形,点 D 为 AB 边上的一点,∠DCE=30°,将线段 CD 绕点 C 顺时针旋转 60°得到线段 CF,连接 AF、EF. 请直接 写出下列结果:
① ∠EAF的度数为__________;
② DE与EF之间的数量关系为__________;
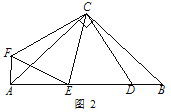
【类比探究】如图 2,△ABC 为等腰直角三角形,∠ACB=90°,点 D 为 AB 边上的一点∠DCE=45°,将线段 CD 绕点 C 顺时针旋转 90°得到线段 CF,连接 AF、EF.
①则∠EAF的度数为__________;
② 线段 AE,ED,DB 之间有什么数量关系?请说明理由;
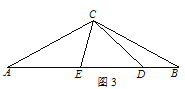
【实际应用】如图 3,△ABC 是一个三角形的余料.小张同学量得∠ACB=120°,AC=BC, 他在边 BC 上取了 D、E 两点,并量得∠BCD=15°、∠DCE=60°,这样 CD、CE 将△
ABC 分成三个小三角形,请求△BCD、△DCE、△ACE 这三个三角形的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华思考解决如下问题:
原题:如图1,点P,Q分别在菱形ABCD的边BC,CD上,∠PAQ=∠B,求证:AP=AQ.
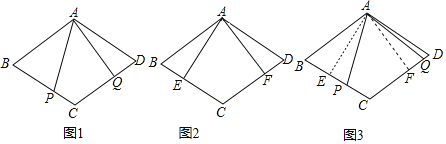
(1)小华进行探索,若将点P,Q的位置特殊化:把∠PAQ绕点A旋转得到∠EAF,使AE⊥BC,点E、F分别在边BC、CD上,如图2.此时她证明了AE=AF,请你证明;
(2)由以上(1)的启发,在原题中,添加辅助线:如图3,作AE⊥BC,AF⊥CD,垂足分别为E,F.请你继续完成原题的证明;
(3)如果在原题中添加条件:AB=4,∠B=60°,如图1,求四边形APCQ的周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
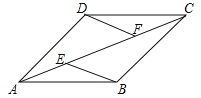
【题目】已知,如图,在四边形ABCD中,AB∥CD,E,F为对角线AC上两点,且AE=CF,DF∥BE,AC平分∠BAD.求证:四边形ABCD为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,∠AOC=90°,
(1)比较∠AOD,∠EOB,∠AOE的大小.
(2)若∠EOC=28°,求∠EOB和∠EOD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
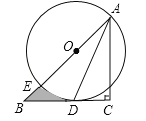
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.
(1)求证:AD平分∠BAC;
(2)若CD=1,求图中阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.
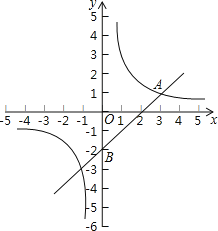
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,3),反比例函数y=![]() 的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
(1)求反比例函数的解析式;
(2)通过计算说明一次函数y=mx+3﹣4m的图象一定过点C;
(3)对于一次函数y=mx+3﹣4m(m≠0),当y随x的增大而增大时,确定点P的横坐标的取值范围,(不必写过程)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com