
【题目】小华思考解决如下问题:
原题:如图1,点P,Q分别在菱形ABCD的边BC,CD上,∠PAQ=∠B,求证:AP=AQ.
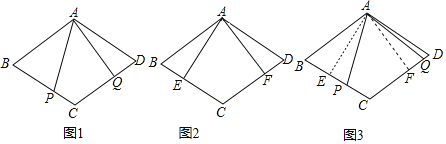
(1)小华进行探索,若将点P,Q的位置特殊化:把∠PAQ绕点A旋转得到∠EAF,使AE⊥BC,点E、F分别在边BC、CD上,如图2.此时她证明了AE=AF,请你证明;
(2)由以上(1)的启发,在原题中,添加辅助线:如图3,作AE⊥BC,AF⊥CD,垂足分别为E,F.请你继续完成原题的证明;
(3)如果在原题中添加条件:AB=4,∠B=60°,如图1,求四边形APCQ的周长的最小值.
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】
(1)根据四边形ABCD是菱形,首先证明∠B=∠D,AB=AD,再结合题意证明![]() ,进而证明△AEB≌△AFD,即可证明AE=AF.
,进而证明△AEB≌△AFD,即可证明AE=AF.
(2)根据(1)的证明,再证明△AEP≌△AFQ(ASA),进而证明AP=AQ.
(3)根据题意连接AC,则可证明△ABC为等边三角形,再计算AE的长度,则可计算长APCQ的周长的最小值.
(1)证明:如图2,∵四边形ABCD是菱形,
∴∠B+∠C=180°,∠B=∠D,AB=AD,
∵∠EAF=∠B,
∴∠EAF+∠C=180°,
∴∠AEC+∠AFC=180°,
∵AE⊥BC,
∴AF⊥CD,
在△AEB和△AFD中,
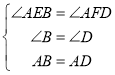 ,
,
∴△AEB≌△AFD(AAS),
∴AE=AF;
(2)证明:如图3,由(1)得,∠PAQ=∠EAF=∠B,AE=AF,
∴∠EAP=∠FAQ,
在△AEP和△AFQ中,
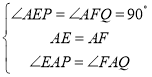 ,
,
∴△AEP≌△AFQ(ASA),
∴AP=AQ;
(3)解:如图4,连接AC,
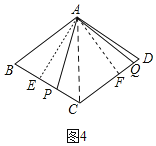
∵∠ABC=60°,BA=BC=4,
∴△ABC为等边三角形,
∵AE⊥BC,
∴BE=EC=2,
同理,CF=FD=2,
∴AE=![]() =2
=2![]() ,
,
∴四边形APCQ的周长=AP+PC+CQ+AQ=2AP+CP+CF+FQ=2AP+2CF,
∵CF是定值,当AP最小时,四边形APCQ的周长最小,
∴当AP=AE时,四边形APCQ的周长最小,此时四边形APCQ的周长的最小值=2×2![]() +4=4
+4=4![]() +4.
+4.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
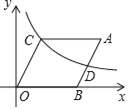
【题目】如图,ABOC放置在直角坐标系中,点A(10,4),点B(6,0),反比例函数y=![]() (x>0)的图象经过点C.
(x>0)的图象经过点C.
(1)求该反比例函数的表达式.
(2)记AB的中点为D,请判断点D是否在该反比例函数的图象上,并说明理由.
(3)若P(a,b)是反比例函数y=![]() 的图象(x>0)的一点,且S△POC<S△DOC,则a的取值范围为_____.
的图象(x>0)的一点,且S△POC<S△DOC,则a的取值范围为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
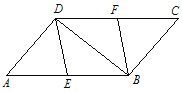
【题目】如图,在□ABCD 中,∠ADB=90°,点 E 为 AB 边的中点,点 F 为CD 边的中点.
(1)求证:四边形 DEBF 是菱形;
(2)当∠A 等于多少度时,四边形 DEBF 是正方形?并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() (k为常数,k≠0)的图象经过点A(2,3).
(k为常数,k≠0)的图象经过点A(2,3).
(1)求这个函数的解析式;
(2)判断点B(-1,6),C(3,2)是否在这个函数的图象上,并说明理由;
(3)当-3<x<-1时,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师在黑板上出了一道解方程的题![]() ,小明马上举手,要求到黑板上做,他是这样做的:
,小明马上举手,要求到黑板上做,他是这样做的:
![]() ……………… …①
……………… …①
![]() …………………… …②
…………………… …②
![]() …………………… …③
…………………… …③
![]() ………………………………… ④
………………………………… ④
![]() ………………………………… ⑤
………………………………… ⑤
老师说:小明解一元一次方程的一般步骤都知道却没有掌握好,因此解题时有一步出现了错误,请你指出他错在 (填编号);
然后,你自己细心地解下面的方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
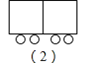
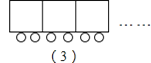
【题目】小明用木棒和硬币拼成如图所示的“列车”形状,第![]() 个图需要
个图需要![]() 根木棒,
根木棒,![]() 枚硬币,第
枚硬币,第![]() 个图需要
个图需要![]() 根木棒,
根木棒,![]() 枚硬币,照这样的方式摆下去,第
枚硬币,照这样的方式摆下去,第![]() 个图需要________根木棒,______枚硬币
个图需要________根木棒,______枚硬币
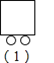
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对全校1200名学生进行“校园安全知识”的教育活动,从1200名学生中随机抽取部分学生进行测试,成绩评定按从高分到低分排列分为![]() ,
, ![]() ,
, ![]() ,
, ![]() 四个等级,绘制了图①、图②两幅不完整的统计图.请结合图中所给信息解答下列问题:
四个等级,绘制了图①、图②两幅不完整的统计图.请结合图中所给信息解答下列问题:
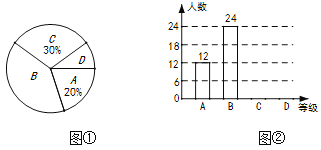
(1)求本次被抽查的学生共有多少名?
(2)将条形统计图和扇形统计图补充完整;
(3)求扇形统计图中“![]() ”所在的扇形圆心角的度数;
”所在的扇形圆心角的度数;
(4)估计全校“![]() ”等级的学生有多少名?
”等级的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
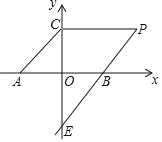
【题目】如图,直线y=x+3与x轴、y轴分别相交于A、C两点,过点B(6,0),E(0,﹣6)的直线上有一点P,满足∠PCA=135°.
(1)求证:四边形ACPB是平行四边形;
(2)求直线BE的解析式及点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人民生活水平的提高,汽车进入家庭的越来越多.我市某小区在2007年底拥有家庭轿车64辆,到了2009年底,家庭轿车数为100辆.
(1)若平均每年轿车数的增长率相同,求这个增长率.
(2)为了缓解停车矛盾,多增加一些车位,该小区决定投资15万元,再造一些停车位.据测算,建造一个室内停车位,需5000元;建造一个室外停车位,需1000元.按实际情况考虑,计划室外停车位数不少于室内车位的2倍,又不能超过室内车位的2.5倍.问,该小区有哪几种建造方案?应选择哪种方案最合理?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com