练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】老师在黑板上出了一道解方程的题，小明马上举手，要求到黑板上做，他是这样做的：

    ……………… …①

    …………………… …②

    …………………… …③

    ………………………………… ④

    ………………………………… ⑤

    老师说：小明解一元一次方程的一般步骤都知道却没有掌握好，因此解题时有一步出现了错误，请你指出他错在 （填编号）；

    然后，你自己细心地解下面的方程：．

    【答案】（1）①；（2）答案见解析．

    【解析】

    （1）小明解方程的第①步中去分母时“1”没有乘以12；

    （2）解带分母的方程，要先去分母、再去括号、最后移项合并同类项，化系数为1，从而得到方程的解．

    解：（1）小明解方程的第①步中去分母时“1”没有乘以12，所以错在①；

    （2），

    去分母，得，

    ∴，

    ∴，

    ∴，

    ∴．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在学校组织的知识竞赛活动中，老师将八年级一班和二班全部学生的成绩整理并绘制成如下统计表：

    得分(分)

    人数(人)

    班级

    50

    60

    70

    80

    90

    100

    一班

    2

    5

    10

    13

    14

    6

    二班

    4

    4

    16

    2

    12

    12

    (1)现已知一班和二班的平均分相同，请求出其平均分．

    (2)请分别求出这两班的中位数和众数，并进一步分析这两个班级在这次竞赛中成绩的情况．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：，．

    （1）求B；(用含a、b的代数式表示)

    （2）比较A与B的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

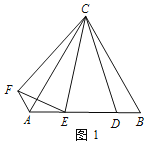
    【题目】【操作发现】如图 1，△ABC 为等边三角形，点 D 为 AB 边上的一点，∠DCE=30°，将线段 CD 绕点 C 顺时针旋转 60°得到线段 CF，连接 AF、EF. 请直接 写出下列结果：

    ① ∠EAF的度数为__________；

    ② DE与EF之间的数量关系为__________；

    【类比探究】如图 2，△ABC 为等腰直角三角形，∠ACB=90°，点 D 为 AB 边上的一点∠DCE=45°，将线段 CD 绕点 C 顺时针旋转 90°得到线段 CF，连接 AF、EF.

    ①则∠EAF的度数为__________；

    ② 线段 AE，ED，DB 之间有什么数量关系？请说明理由；

    【实际应用】如图 3，△ABC 是一个三角形的余料.小张同学量得∠ACB=120°，AC=BC， 他在边 BC 上取了 D、E 两点，并量得∠BCD=15°、∠DCE=60°，这样 CD、CE 将△

    ABC 分成三个小三角形，请求△BCD、△DCE、△ACE 这三个三角形的面积之比.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某自行车厂一周计划生产辆自行车，平均每天生产辆，由于各种原因实际每天生产量与计划量相比有出入，下表是某周的生产情况（超产为正，减产为负）；

    星期

    一

    二

    三

    四

    五

    六

    日

    增减

    根据记录可知前三天共生产________辆；

    产量最多的一天比产量最少的一天多生产________辆；

    该厂实行计件工资制，每辆车元，超额完成任务每辆奖元，少生产一辆扣元，那么该厂工人这一周的工资总额是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小华思考解决如下问题：

    原题：如图1，点P，Q分别在菱形ABCD的边BC，CD上，∠PAQ＝∠B，求证：AP＝AQ．

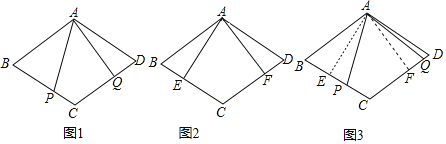
    （1）小华进行探索，若将点P，Q的位置特殊化：把∠PAQ绕点A旋转得到∠EAF，使AE⊥BC，点E、F分别在边BC、CD上，如图2．此时她证明了AE＝AF，请你证明；

    （2）由以上（1）的启发，在原题中，添加辅助线：如图3，作AE⊥BC，AF⊥CD，垂足分别为E，F．请你继续完成原题的证明；

    （3）如果在原题中添加条件：AB＝4，∠B＝60°，如图1，求四边形APCQ的周长的最小值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，如图，在四边形ABCD中，AB∥CD，E，F为对角线AC上两点，且AE=CF，DF∥BE，AC平分∠BAD．求证：四边形ABCD为菱形．

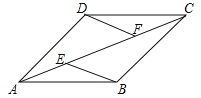
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠C=90°，AC=BC，点O在AB上，经过点A的⊙O与BC相切于点D，交AB于点E．

    （1）求证：AD平分∠BAC；

    （2）若CD=1，求图中阴影部分的面积（结果保留π）．

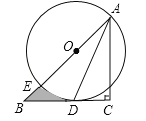
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一般地，任何一个无限循环小数都可以写成分数形式，如0.＝0.777…，它的循环节有一位，设0. ＝x，由0. ＝0777…，可知，10x＝7.777…，所以10x﹣x＝7，得x＝．于是，得0. ＝，再如0.＝0.737373…，它的循环节有两位，设0.＝x，由0.＝0.737373…可知，100x＝73.7373…，所以100x﹣x＝73．解方程得x＝．于是，得0. ＝，类比上述方法，无限循环小数0. 3化为分数形式为_____．

    查看答案和解析>>

    同步练习册答案