【题目】如图，直线AB，CD相交于点O，∠AOC=90°，
(1)比较∠AOD，∠EOB，∠AOE的大小.
(2)若∠EOC=28°，求∠EOB和∠EOD的度数.
【答案】（1）∠AOE＜∠AOD＜∠BOE；（2）∠EOB=118°，∠EOD=152°.
【解析】
（1）由∠AOC=90°，得出∠AOD=90°，∠EOB＞90°，∠AOE＜90°，即可得出答案；
（2）由∠AOC=90°，可得∠BOC=90°，再通过∠EOB=∠BOC+∠EOC，∠EOC=28°，即可求出∠EOB；由∠EOD=180°-∠EOC，即可求出∠EOD．
解：（1）∵∠AOC=90°，直线AB，CD相交于点O，
∴∠AOC=∠AOD=∠BOD=∠BOC=90°，
∴∠AOD=90°，∠EOB＞90°，∠AOE＜90°，
即∠AOE＜∠AOD＜∠BOE．
（2）由∠AOC=90°，可得∠BOC=90°，
∵∠EOC=28°，
∴∠EOB=∠BOC+∠EOC=90°+28°=118°，
由已知可得∠EOD=180°-∠EOC=180°-28°=152°.
科目：初中数学 来源： 题型：
【题目】已知反比例函数
（k为常数，k≠0）的图象经过点A（2，3）．
（1）求这个函数的解析式；
（2）判断点B（－1，6），C（3，2）是否在这个函数的图象上，并说明理由；
（3）当－3＜x＜－1时，求y的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
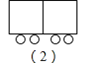
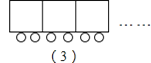
【题目】小明用木棒和硬币拼成如图所示的“列车”形状，第
个图需要
根木棒，
枚硬币，第个图需要
根木棒，枚硬币，照这样的方式摆下去，第
个图需要________根木棒，______枚硬币
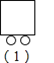
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学对全校1200名学生进行“校园安全知识”的教育活动，从1200名学生中随机抽取部分学生进行测试，成绩评定按从高分到低分排列分为
， 
， 
， 
四个等级，绘制了图①、图②两幅不完整的统计图．请结合图中所给信息解答下列问题：
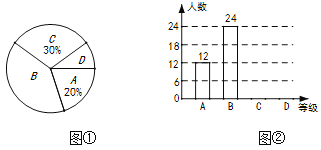
（1）求本次被抽查的学生共有多少名？
（2）将条形统计图和扇形统计图补充完整；
（3）求扇形统计图中“
”所在的扇形圆心角的度数；
（4）估计全校“
”等级的学生有多少名？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】出租车司机王师傅从上午8:10~9:25在合肥市巢湖大堤环岛路上一段东西方向路段上营运，共连续运载十批乘客.若规定向东为正，向西为负，王师傅运载十批乘客的里程如下：（单位：千米）+9，-7，+3，-8，+8，+5，-9，-4，+4，+3
（1）将最后一批乘客送到目的地时，王师傅距离第一批乘客出发地的位置怎样？距离多少千米？
（2）上午8:10~9:25王师傅开车的平均速度是多少？
（3）若出租车的收费标准为：起步价8元（不超过3千米），超过3千米，超过部分每千米1.5元.则王师傅在上午8:10~9:25一共收入多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
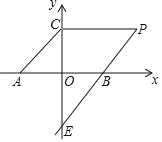
【题目】如图，直线y＝x+3与x轴、y轴分别相交于A、C两点，过点B（6，0），E（0，﹣6）的直线上有一点P，满足∠PCA＝135°．
（1）求证：四边形ACPB是平行四边形；
（2）求直线BE的解析式及点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知代数式
，当
时，该代数式的值为3．
（1）求c的值；
（2）已知：当
时，该代数式的值为0.
①求：当
时，该代数式的值；
②若
，
，
，试比较a与d的大小，并说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在直角坐标平面内，直线y=
x+2分别与x轴、y轴交于点A、C．抛物线y=﹣
+bx+c经过点A与点C，且与x轴的另一个交点为点B．点D在该抛物线上，且位于直线AC的上方．
（1）求上述抛物线的表达式；
（2）联结BC、BD，且BD交AC于点E，如果△ABE的面积与△ABC的面积之比为4：5，求∠DBA的余切值；
（3）过点D作DF⊥AC，垂足为点F，联结CD．若△CFD与△AOC相似，求点D的坐标．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
