
【题目】在直角坐标平面内,直线y=![]() x+2分别与x轴、y轴交于点A、C.抛物线y=﹣
x+2分别与x轴、y轴交于点A、C.抛物线y=﹣![]() +bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.
+bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.
(1)求上述抛物线的表达式;
(2)联结BC、BD,且BD交AC于点E,如果△ABE的面积与△ABC的面积之比为4:5,求∠DBA的余切值;
(3)过点D作DF⊥AC,垂足为点F,联结CD.若△CFD与△AOC相似,求点D的坐标.

【答案】(1)y=﹣![]() x+2;(2)
x+2;(2)![]() ;(3)(﹣
;(3)(﹣![]() ,
,![]() )或(﹣3,2).
)或(﹣3,2).
【解析】试题分析:(1)由直线得到A、C的坐标,然后代入二次函数解析式,利用待定系数法即可得;
(2)过点E作EH⊥AB于点H,由已知可得![]() ,从而可得
,从而可得![]() 、
、![]() 的长,然后再根据三角函数的定义即可得;
的长,然后再根据三角函数的定义即可得;
(3)分情况讨论即可得.
试题分析:(1)由已知得A(-4,0),C(0,2) ,
把A、C两点的坐标代入![]() 得,
得,
![]() ,∴
,∴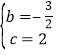 ,
,
∴![]() ;
;
(2)过点E作EH⊥AB于点H,
由上可知B(1,0), ∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ∴
∴![]() ,
,
∵![]() ∴
∴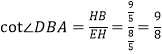 ;
;
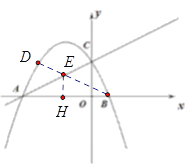
(3)∵DF⊥AC , ∴![]() ,
,
①若![]() ,则CD//AO , ∴点D的纵坐标为2,
,则CD//AO , ∴点D的纵坐标为2,
把y=2代入![]() 得x=-3或x=0(舍去),
得x=-3或x=0(舍去),
∴D(-3,2) ;
②若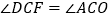 时,过点D作DG⊥y轴于点G,过点C作CQ⊥DG交x轴于点Q,
时,过点D作DG⊥y轴于点G,过点C作CQ⊥DG交x轴于点Q,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
设Q(m,0),则![]() , ∴
, ∴![]() , ∴
, ∴![]() ,
,
易证:![]() ∽
∽![]() ,∴
,∴![]() ,
,
设D(-4t,3t+2)代入![]() 得t=0(舍去)或者
得t=0(舍去)或者![]() ,
,
∴![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,把矩形OABC放入平面直角坐标系xO中,使OA、OC分别落在x、y轴的正半轴上,其中AB=15,对角线AC所在直线解析式为y=﹣![]() x+b,将矩形OABC沿着BE折叠,使点A落在边OC上的点D处.
x+b,将矩形OABC沿着BE折叠,使点A落在边OC上的点D处.
(1)求点B的坐标;
(2)求EA的长度;
(3)点P是y轴上一动点,是否存在点P使得△PBE的周长最小,若存在,请求出点P的坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推进书香校园建设,加强学生课外阅读,某校开展了“走近名家名篇”的主题活动;学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频数分布表和频数分布直方图的一部分,如下:
时间(单位: | 频数(人数) | 频率 |
| 2 | 0.04 |
| 3 | 0.06 |
| 15 | 0.30 |
|
| 0.50 |
| 5 |
|

请根据图表信息回答下列问题:
(1)频数分布表中的![]() _________,
_________,![]() ___________;
___________;
(2)将频数分布直方图补充完整;
(3)学校将每周课外阅读时间在8小时以上的学生评为“阅读之星”,请你估计该校1200名学生中评为“阅读之星”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,![]() ,点P为AC边上一点,将线段AP绕点A顺时针方向旋转,当AP旋转至
,点P为AC边上一点,将线段AP绕点A顺时针方向旋转,当AP旋转至![]() 时,点
时,点![]() 恰好在同一直线上,此时
恰好在同一直线上,此时![]() 于点E.
于点E.

(1)求证:![]()
(2)若![]() ,求AE的长
,求AE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小强从A处出发沿北偏东70°方向行走,走至B处,又沿着北偏西30°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是( )
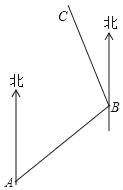
A. 左转 80° B. 右转80° C. 右转 100° D. 左转 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C 为线段 AD 上一点,B 为 CD 的中点,AD=13cm,BD=3cm.
(1)图中共有 条线段;
(2)求 AC 的长;
(3)若点 E 在线段 AD 上,且 BE=2cm,求 AE 的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三张形状、大小相同但画面不同的风景图片,都按同样的方式剪成相同的三段,然后将上、中、下三段分别混合洗匀,从三堆图片中随机各抽出一张, 求这三张图片恰好组成一张完整风景图片的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知正方形ABCD和正方形AEFG有公共顶点A,连接BE,DG.


(1)问:BE与DG有什么关系?说明理由.
(2)如图2,已知AB=4,AE=![]() ,当点F在边AD上时,求BE的长.
,当点F在边AD上时,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com