Question

【题目】如图1，已知正方形ABCD和正方形AEFG有公共顶点A，连接BE，DG．

　　　

（1）问：BE与DG有什么关系？说明理由．

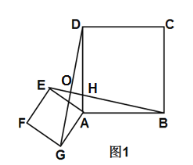
（2）如图2，已知AB=4，AE=，当点F在边AD上时，求BE的长．

Answer 1

【答案】（1）BE=DG且BE⊥DG；理由见解析；（2）BE=．

【解析】

（1）设BE和DG相交于点O，AD和BE相交于点H，根据正方形的性质，可得AD=AB，AG=AE，∠DAB=∠EAG=90，利用SAS证明△EAB≌△GAD，得出BE=DG，∠GDA=∠EBA，推出∠DOH=∠HAB=90，即可求得．

（2）过点E作EM，已知四边形AEFG是正方形，四边形ABCD是正方形，∠EAF=∠FAG=45，∠DAB=90，可得∠EAM=45，已知AE，即可求得AM，BM，利用勾股定理即可求出BE．

（1）设BE和DG相交于点O，AD和BE相交于点H

∵四边形ABCD是正方形

∴AD=AB，∠DAB=90

∵四边形AEFG是正方形

∴AG=AE，∠EAG=90

∴∠EAB=∠EAD+∠DAB=∠EAD+∠EAG=∠GAD

∴

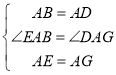
∴△EAB≌△GAD

∴BE=DG，∠GDA=∠EBA

∵∠DHO=∠BHA

∴∠DOH=∠HAB==90

∴BE⊥DG

故答案为：BE=DG且BE⊥DG

（2）过点E作EM

∵四边形AEFG是正方形

∴∠EAF=∠FAG=45

∵∵四边形ABCD是正方形

∴∠DAB=90

∴∠EAM=45

∴AM=EM

∵

∴

∴AM=1

∴MB=AB-AM=4-1=3

∴

故答案为：