
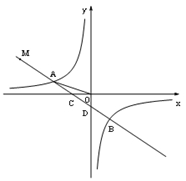
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() 两点,与
两点,与![]() 轴、
轴、![]() 轴分别交于C、D两点.已知:
轴分别交于C、D两点.已知: ![]() ,点B的坐标为
,点B的坐标为![]() .
.
(1)求该反比例函数的解析式和点D的坐标;
(2)点M在射线CA上,且MA=2AC,求△MOB的面积.
【答案】(1)![]() ,D(0,-1);(2)
,D(0,-1);(2)![]()
【解析】试题分析:(1)过A作AE⊥x轴于点E,在Rt△AOE中,可根据OA的长求得A点坐标,代入反比例函数解析式可求反比例函数解析式,进一步可求得B点坐标,利用待定系数法可求得直线AB的解析式,则可求得D点坐标;(2)过M作MF⊥x轴于点F,可证得△MFC∽△AEC,可求得MF的长,代入直线AB解析式可求得M点坐标,进一步可求得△MOB的面积.
试题解析:
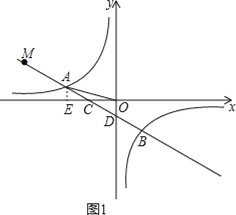
(1)如图1,过A作AE⊥x轴于E,
在Rt△AOE中,tan∠AOC=![]() ,
,
设AE=a,则OE=3a,
∴OA=![]() =
=![]() a,
a,
∵OA=![]() ,
,
∴a=1,
∴AE=1,OE=3,
∴A点坐标为(﹣3,1),
∵反比例函数y2=![]() (k≠0)的图象过A点,
(k≠0)的图象过A点,
∴k=﹣3,
∴反比例函数解析式为y2=﹣![]() ,
,
∵反比例函数y2=﹣![]() 的图象过B(
的图象过B(![]() ,m),
,m),
∴![]() m=﹣3,解得m=﹣2,
m=﹣3,解得m=﹣2,
∴B点坐标为(![]() ,﹣2),
,﹣2),
设直线AB解析式为y=nx+b,把A、B两点坐标代入可得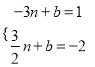 ,
,
解得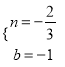 ,
,
∴直线AB的解析式为y=﹣![]() x﹣1,
x﹣1,
令x=1,可得y=﹣1,
∴D点坐标为(0,﹣1);
(2)由(1)可得AE=1,
∵MA=2AC,
∴![]() ,
,
如图2,过M作MF⊥x轴于点F,则△CAE∽△CMF,
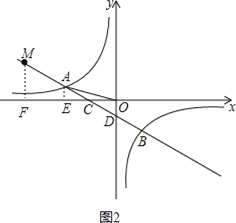
∴![]() ,
,
∴MF=3,即M点的纵坐标为3,
代入直线AB解析式可得3=﹣![]() x﹣1,解得x=﹣6,
x﹣1,解得x=﹣6,
∴M点坐标为(﹣6,3),
∴S△MOB=![]() OD(xB﹣xM)=
OD(xB﹣xM)=![]() ×1×(
×1×(![]() +6)=
+6)=![]() ,
,
即△MOB的面积为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.
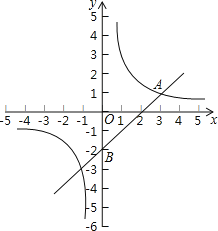
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点A(1,0),B(4,1),C(4,3),反比例函数y=![]() 的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
的图象经过点D,点P是一次函数y=mx+3﹣4m(m≠0)的图象与该反比例函数图象的一个公共点;
(1)求反比例函数的解析式;
(2)通过计算说明一次函数y=mx+3﹣4m的图象一定过点C;
(3)对于一次函数y=mx+3﹣4m(m≠0),当y随x的增大而增大时,确定点P的横坐标的取值范围,(不必写过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】树人学校实施新课程改革以来,学生的学习能力有了很大提高.周老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差)后,再将调查结果绘制成两幅不完整的统计图(如图).请根据统计图解答下列问题:

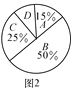
(1)本次调查中,周老师一共调查了________名学生,扇形统计图中“较差”部分的圆心角是__________;
(2)将条形统计图补充完整;
(3)如果树人学校共有6000名学生,“特别好”的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,旗杆AB的顶端B在夕阳的余辉下落在一个斜坡上的点D处,某校数学课外兴趣小组的同学正在测量旗杆的高度,在旗杆的底部A处测得点D的仰角为15°,AC=10米,又测得∠BDA=45°.已知斜坡CD的坡度为i=1:![]() ,求旗杆AB的高度(
,求旗杆AB的高度(![]() ≈1.7,结果精确到个位).
≈1.7,结果精确到个位).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学实践活动中,观测小组对某品牌节能饮水机进行了观察和记录,当观察到第![]() 分钟时,水温为
分钟时,水温为![]() ,记录的相关数据如下表所示:
,记录的相关数据如下表所示:
第一次加热、降温过程 | … | |||||||||||
t(分钟) | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | … |
y( | 20 | 40 | 60 | 80 | 100 | 80 | 66.7 | 57.1 | 50 | 44.4 | 40 | … |
(饮水机功能说明:水温加热到![]() 时饮水机停止加热,水温开始下降,当降到
时饮水机停止加热,水温开始下降,当降到![]() 时饮水机又自动开始加热)
时饮水机又自动开始加热)
请根据上述信息解决下列问题:
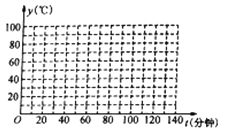
(1)根据表中数据在如给出的坐标系中,描出相应的点;
(2)选择适当的函数,分别求出第一次加热过程和第一次降温过程![]() 关于
关于![]() 的函数关系式,并写出相应自变量的取值范围;
的函数关系式,并写出相应自变量的取值范围;
(3)已知沏茶的最佳水温是![]() ,若18:00开启饮水机(初始水温
,若18:00开启饮水机(初始水温![]() )到当晚20:10,沏茶的最佳水温时间共有多少分钟?
)到当晚20:10,沏茶的最佳水温时间共有多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市某中学开展以“三创一办”为中心,以“校园文明”为主题的手抄报比赛.同学们积极参与,参赛同学每人交了一份得意作品,所有参赛作品均获奖,奖项分为一等奖、二等奖、三等奖和优秀奖,将获奖结果绘制成如下两幅统计图.请你根据图中所给信息解答下列问题:
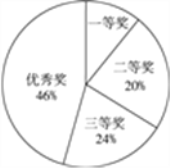

(1)一等奖所占的百分比是__________.
(2)在此次比赛中,一共收到多少份参赛作品?请将条形统计图补充完整.
(3)各奖项获奖学生分别有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某施工小组乘-辆汽车在东西走向的公路上进行建设,约定向东走为正,某大从![]() 地出发到收工时的行走记录如下(单位:
地出发到收工时的行走记录如下(单位: ![]() );
);![]() ,
,![]() ,求:
,求:
(1)问收工时施工小组是否回到![]() 地,如果回到
地,如果回到![]() 地,请说明理由;如果没有回到
地,请说明理由;如果没有回到![]() 地,请说明检修小组最后的位置:
地,请说明检修小组最后的位置:
(2)距离![]() 地最远的是哪一次?距离多远?
地最远的是哪一次?距离多远?
(3)若汽车每千米耗油![]() 升,开工时储油
升,开工时储油![]() 升,到收工时,中途是否需要加油,若加油最少加多少升?若不需要加油,到收工时,还剩多少升汽油? (假定汽车可以开到油量为
升,到收工时,中途是否需要加油,若加油最少加多少升?若不需要加油,到收工时,还剩多少升汽油? (假定汽车可以开到油量为![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下表(注:水费按月份结算,![]() 表示立方米).
表示立方米).
每月用水量 | 单价 |
不超过 | 2元/ |
超出 | 4元/ |
超出 | 8元/ |
请根据上表的内容解答下列问题:
(1)若某户居民2月份用水![]() ,则应收水费_________.元
,则应收水费_________.元
(2)若该户居民3月份用水![]() (其中
(其中![]() ),则应收水费多少元(用含a的代数式表示,并简化).
),则应收水费多少元(用含a的代数式表示,并简化).
(3)若该户居民4,5两个月共用水![]() (5月份用水量超过了4月份),设4月份,用水
(5月份用水量超过了4月份),设4月份,用水![]() ,则该户居民4,5两个月共交水费多少元(用含x的代数式表示,并简化).
,则该户居民4,5两个月共交水费多少元(用含x的代数式表示,并简化).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com