
【题目】树人学校实施新课程改革以来,学生的学习能力有了很大提高.周老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差)后,再将调查结果绘制成两幅不完整的统计图(如图).请根据统计图解答下列问题:

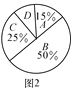
(1)本次调查中,周老师一共调查了________名学生,扇形统计图中“较差”部分的圆心角是__________;
(2)将条形统计图补充完整;
(3)如果树人学校共有6000名学生,“特别好”的有多少人?
【答案】(1)20,36°;(2)详见解析;(3)900.
【解析】试题分析:(1)用特别好的学生人数除以特别好的学生人数所占的百分比即可得这次调查的学生人数;根据扇形统计图求得较差学生所占的百分比,用360°乘以较差学生所占的百分比即可;(2)求得一般和较差学生的人数,再求得一般学生中的女生人数和较差学生中的男生人数,补全统计图即可;(3)用总人数乘以特别好学生所占的百分比即可.
试题解析:
(1)(2+1)÷15%=20(人);
360°×(1-50%-25%-15%)=36°;
故答案为:20,36°;
(2)20×25%=5(人),5-2=3人;
20×(1-50%-25%-15%)=2(人),2-1=1人;
补图如下:
(3)6000×15%=900(人),
答:“特别好”的有900人.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
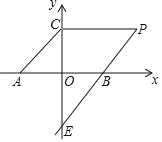
【题目】如图,直线y=x+3与x轴、y轴分别相交于A、C两点,过点B(6,0),E(0,﹣6)的直线上有一点P,满足∠PCA=135°.
(1)求证:四边形ACPB是平行四边形;
(2)求直线BE的解析式及点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人民生活水平的提高,汽车进入家庭的越来越多.我市某小区在2007年底拥有家庭轿车64辆,到了2009年底,家庭轿车数为100辆.
(1)若平均每年轿车数的增长率相同,求这个增长率.
(2)为了缓解停车矛盾,多增加一些车位,该小区决定投资15万元,再造一些停车位.据测算,建造一个室内停车位,需5000元;建造一个室外停车位,需1000元.按实际情况考虑,计划室外停车位数不少于室内车位的2倍,又不能超过室内车位的2.5倍.问,该小区有哪几种建造方案?应选择哪种方案最合理?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标平面内,直线y=![]() x+2分别与x轴、y轴交于点A、C.抛物线y=﹣
x+2分别与x轴、y轴交于点A、C.抛物线y=﹣![]() +bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.
+bx+c经过点A与点C,且与x轴的另一个交点为点B.点D在该抛物线上,且位于直线AC的上方.
(1)求上述抛物线的表达式;
(2)联结BC、BD,且BD交AC于点E,如果△ABE的面积与△ABC的面积之比为4:5,求∠DBA的余切值;
(3)过点D作DF⊥AC,垂足为点F,联结CD.若△CFD与△AOC相似,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
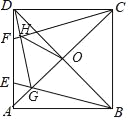
【题目】如图,四边形ABCD是正方形,AC与BD,相交于点O,点E、F是边AD上两动点,且AE=DF,BE与对角线AC交于点G,联结DG,DG交CF于点H.
(1)求证:∠ADG=∠DCF;
(2)联结HO,试证明HO平分∠CHG.
查看答案和解析>>
科目:初中数学 来源: 题型:
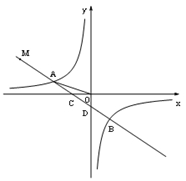
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() 两点,与
两点,与![]() 轴、
轴、![]() 轴分别交于C、D两点.已知:
轴分别交于C、D两点.已知: ![]() ,点B的坐标为
,点B的坐标为![]() .
.
(1)求该反比例函数的解析式和点D的坐标;
(2)点M在射线CA上,且MA=2AC,求△MOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,有下列条件:①AB![]() CD;②AD
CD;②AD![]() BC;③AC=BD;④AC⊥BD.
BC;③AC=BD;④AC⊥BD.
(1)从中任选一个作为已知条件,能判定四边形ABCD是平行四边形的概率是 .
(2)从中任选两个作为已知条件,请用画树状图或列表的方法表示能判定四边形ABCD是矩形的概率,并判断四边形ABCD是菱形的概率?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD,CEFG按如图放置,点B,C,E在同一条直线上,点P在BC边上,PA=PF,且∠APF=90°,连接AF交CD于点M,有下列结论:①EC=BP;②AP=AM;③∠BAP=∠GFP;④AB2+CE2=![]() AF2;⑤S正方形ABCD+S正方形CEFG=2S△APF.其中正确的是( )
AF2;⑤S正方形ABCD+S正方形CEFG=2S△APF.其中正确的是( )
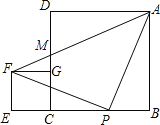
A. ①②③ B. ①③④ C. ①②④⑤ D. ①③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com