
ΓΨΧβΡΩΓΩ–Γ¥œ‘ΎΗ¥œΑΙΐ≥Χ÷–Θ§ΖΔœ÷ ΐ÷α…œœΏΕΈΒΡ≥ΛΕ»Ω…“‘”ΟœΏΕΈΕΥΒψ±μ ΨΒΡ ΐΫχ––ΦθΖ®‘ΥΥψΒΟΒΫΘ§άΐΘΚ
»γΆΦ1Θ§œΏΕΈ![]() Θ§œΏΕΈ
Θ§œΏΕΈ![]() Θ§
Θ§

œΏΕΈ![]() Θ§œΏΕΈ
Θ§œΏΕΈ![]()
Ϋα¬έΘΚ ΐ÷α…œ»Έ“βΝΫΒψ±μ ΨΒΡ ΐΖ÷±πΈΣΘΚ![]() Θ§
Θ§![]() Θ®
Θ®![]() Θ©Θ§‘ρ’βΝΫΒψΦδΒΡΨύάκΈΣΘΚ
Θ©Θ§‘ρ’βΝΫΒψΦδΒΡΨύάκΈΣΘΚ![]() Θ®Φ¥ΘΚΫœ¥σΒΡ ΐΦθ»ΞΫœ–ΓΒΡ ΐΘ©.
Θ®Φ¥ΘΚΫœ¥σΒΡ ΐΦθ»ΞΫœ–ΓΒΡ ΐΘ©.
≥Δ ‘”Π”ΟΘΚ
Θ®1Θ©»τ ΐ÷α…œΒψ![]() Θ§Βψ
Θ§Βψ![]() ¥ζ±μΒΡ ΐΖ÷±π «Θ≠3Θ§Θ≠1Θ§‘ρ
¥ζ±μΒΡ ΐΖ÷±π «Θ≠3Θ§Θ≠1Θ§‘ρ![]() ______.
______.
Θ®2Θ©Α―“ΜΧθ ΐ÷α‘Ύ ΐ![]() ¥ΠΕ‘’έΘ§±μ ΨΘ≠9ΚΆ3ΝΫ ΐΒΡΒψ«ΓΚΟΜΞœύ÷ΊΚœΘ§¥Υ ±
¥ΠΕ‘’έΘ§±μ ΨΘ≠9ΚΆ3ΝΫ ΐΒΡΒψ«ΓΚΟΜΞœύ÷ΊΚœΘ§¥Υ ±![]() ______.
______.
Θ®3Θ© ΐ÷α…œΒΡΝΫΗωΒψ÷°ΦδΒΡΨύάκΈΣ6Θ§Τδ÷–“ΜΗωΒψ±μ ΨΒΡ ΐΈΣ3Θ§Νμ“ΜΗωΒψ±μ ΨΒΡ ΐΈΣ![]() Θ§‘ρ
Θ§‘ρ![]() ______.
______.
Έ ΧβΫβΨωΘΚ
Θ®4Θ©»γΆΦ2Θ§Βψ![]() ±μ Ψ ΐ
±μ Ψ ΐ![]() Θ§Βψ
Θ§Βψ![]() ±μ ΨΘ≠2Θ§Βψ
±μ ΨΘ≠2Θ§Βψ![]() ±μ Ψ
±μ Ψ![]() «“
«“![]() Θ§Έ Βψ
Θ§Έ Βψ![]() ΚΆΒψ
ΚΆΒψ![]() Ζ÷±π±μ Ψ ≤Ο¥ ΐΘΩΈΣ ≤Ο¥ΘΩ
Ζ÷±π±μ Ψ ≤Ο¥ ΐΘΩΈΣ ≤Ο¥ΘΩ

Θ®5Θ©…œ ωΘ®4Θ©ΒΡΧθΦΰœ¬Θ§ΆΦ2Υυ ΨΒΡ ΐ÷α…œΘ§ «Ζώ¥φ‘Ύ¬ζΉψΧθΦΰΒΡΒψ![]() Θ§ Ι”Ο
Θ§ Ι”Ο![]() ΘΩ
ΘΩ
»τ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ω![]() Υυ±μ ΨΒΡ ΐΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΩΘ®Βψ
Υυ±μ ΨΒΡ ΐΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΩΘ®Βψ![]() ≤Μ”κΒψ
≤Μ”κΒψ![]() Θ§Βψ
Θ§Βψ![]() Θ§Βψ
Θ§Βψ![]() ÷ΊΚœΘ©
÷ΊΚœΘ©
ΓΨ¥πΑΗΓΩΘ®1Θ©2ΘΜΘ®2Θ©Θ≠3ΘΜΘ®3Θ©Θ≠3Μρ9ΘΜΘ®4Θ©Βψ![]() ±μ ΨΘ≠3Θ§Βψ
±μ ΨΘ≠3Θ§Βψ![]() ±μ Ψ2ΘΜΘ®5Θ©
±μ Ψ2ΘΜΘ®5Θ©![]() ΜρΘ≠5.
ΜρΘ≠5.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΒψFΓΔE¥ζ±μΒΡ ΐΖ÷±πΈΣ-1ΚΆ-3Θ§Ω…ΒΟœΏΕΈEF=-1-Θ®-3Θ©=2ΘΜ
Θ®2Θ©”…Χβ“βΩ…÷Σ![]() «Θ≠9ΚΆ3ΒΡ÷–ΒψΘ§Ψί¥ΥΩ…ΫβΘΜ
«Θ≠9ΚΆ3ΒΡ÷–ΒψΘ§Ψί¥ΥΩ…ΫβΘΜ
Θ®3Θ©Ζ÷ΝΫ÷÷«ιΩωΧ÷¬έΘ§3-n=6Μρn-3=6Θ§ΫβΖΫ≥ΧΦ¥Ω…ΘΜ
Θ®4Θ©œ»±μ Ψ≥ωBCΚΆABΘ§‘ΌΗυΨί![]() Ν–≥ωΖΫ≥ΧΘ§Ϋβ÷°Φ¥Ω…ΘΜ
Ν–≥ωΖΫ≥ΧΘ§Ϋβ÷°Φ¥Ω…ΘΜ
Θ®5Θ©Ζ÷ΥΡ÷÷«ιΩωΔΌΒ±Βψ![]() ‘ΎΒψ
‘ΎΒψ![]() ”“≤ύ ±ΘΜΔΎΒ±Βψ
”“≤ύ ±ΘΜΔΎΒ±Βψ![]() ‘ΎΒψ
‘ΎΒψ![]() ”κ
”κ![]() ÷°Φδ ±;ΔέΒ±Βψ
÷°Φδ ±;ΔέΒ±Βψ![]() ‘ΎΒψ
‘ΎΒψ![]() ”κ
”κ![]() ÷°Φδ ±ΘΜΔήΒ±Βψ
÷°Φδ ±ΘΜΔήΒ±Βψ![]() ‘ΎΒψ
‘ΎΒψ![]() Ήσ≤ύ ±.
Ήσ≤ύ ±.
ΫβΘΚ≥Δ ‘”Π”ΟΘ®1Θ©EF=-1-Θ®-3Θ©=2ΘΜ
Θ®2Θ©”…Χβ“βΩ…÷Σ3-m=m-(-9)
Γύm=Θ≠3;
Θ®3Θ©”…Χβ“βΩ…÷Σ3-n=6Μρn-3=6Θ§
Γύn=Θ≠3Μρn=9;
Έ ΧβΫβΨωΘΚ
Θ®4Θ©ΓΏ![]() Θ§
Θ§![]()
”÷ΓΏ![]()
Γύ![]()
Γύ![]() ,
,
ΓύΒψ![]() ±μ ΨΘ≠3Θ§Βψ
±μ ΨΘ≠3Θ§Βψ![]() ±μ Ψ2;
±μ Ψ2;
Θ®5Θ©…ηΒψ![]() ±μ ΨΒΡ ΐ «
±μ ΨΒΡ ΐ «![]() Θ§
Θ§
ΔΌΒ±Βψ![]() ‘ΎΒψ
‘ΎΒψ![]() ”“≤ύ ±Θ§
”“≤ύ ±Θ§![]()
Γύ![]() Θ®≤ΜΖϊΚœΧβ“βΘ©;
Θ®≤ΜΖϊΚœΧβ“βΘ©;
ΔΎΒ±Βψ![]() ‘ΎΒψ
‘ΎΒψ![]() ”κ
”κ![]() ÷°Φδ ±Θ§
÷°Φδ ±Θ§![]()
Γύ![]() ;
;
ΔέΒ±Βψ![]() ‘ΎΒψ
‘ΎΒψ![]() ”κ
”κ![]() ÷°Φδ ±Θ§
÷°Φδ ±Θ§![]()
Γύ![]() Θ®≤ΜΖϊΚœΧβ“βΘ©
Θ®≤ΜΖϊΚœΧβ“βΘ©
ΔήΒ±Βψ![]() ‘ΎΒψ
‘ΎΒψ![]() Ήσ≤ύ ±Θ§
Ήσ≤ύ ±Θ§![]()
Γύ![]() ;
;
Ι ¥φ‘ΎΒψ![]() ±μ ΨΒΡ ΐ «
±μ ΨΒΡ ΐ «![]() ΜρΘ≠5.
ΜρΘ≠5.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ![]() Θ§
Θ§![]() Θ°
Θ°
Θ®1Θ©«σBΘΜ(”ΟΚ§aΓΔbΒΡ¥ζ ΐ Ϋ±μ Ψ)
Θ®2Θ©±»ΫœA”κBΒΡ¥σ–ΓΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
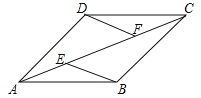
ΓΨΧβΡΩΓΩ“―÷ΣΘ§»γΆΦΘ§‘ΎΥΡ±Ώ–ΈABCD÷–Θ§ABΓΈCDΘ§EΘ§FΈΣΕ‘Ϋ«œΏAC…œΝΫΒψΘ§«“AE=CFΘ§DFΓΈBEΘ§ACΤΫΖ÷ΓœBADΘ°«σ÷ΛΘΚΥΡ±Ώ–ΈABCDΈΣΝβ–ΈΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
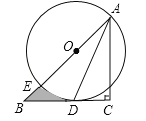
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœC=90ΓψΘ§AC=BCΘ§ΒψO‘ΎAB…œΘ§Ψ≠ΙΐΒψAΒΡΓ―O”κBCœύ«–”ΎΒψDΘ§ΫΜAB”ΎΒψEΘ°
Θ®1Θ©«σ÷ΛΘΚADΤΫΖ÷ΓœBACΘΜ
Θ®2Θ©»τCD=1Θ§«σΆΦ÷–“θ”Α≤ΩΖ÷ΒΡΟφΜΐΘ®ΫαΙϊ±ΘΝτΠ–Θ©Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΚκ―ο÷–ΜΣ”≈–ψ¥ΪΆ≥ΈΡΜ·,Ρ≥÷–―ß‘Ύ2019Ρξ‘ΣΒ©«ΑœΠ,”…–ΘΆ≈Έ·Ήι÷·»Ϊ–Θ―ß…ζΩΣ’ΙΝΥ“Μ¥Έ ιΖ®±»»ϋΈΣΝΥ±μ’Ο ιΖ®±»»ϋ÷–ΒΡΜώΫ±―ß…ζ,ΦΤΜ°ΙΚ¬ρΗ÷± 30÷ß,ΟΪ± 20÷ß,Ι≤–η1070‘Σ,Τδ÷–ΟΩ÷ßΟΪ± ±»Η÷± Ισ6‘Σ.
(1)«σΗ÷± ΚΆΟΪ± ΒΡΒΞΦέΗςΈΣΕύ…Ό‘Σ?
(2)Κσά¥–ΘΆ≈Έ·ΨωΕ®Βς’ϊ…ηΫ±ΖΫΑΗ,ά©¥σ±μ’ΟΟφ,–η“ΣΙΚ¬ρ…œΟφΒΡΝΫ÷÷± Ι≤60÷ß(ΟΩ÷÷± ΒΡΒΞΦέ≤Μ±δ)’≈άœ ΠΉωΆξ‘ΛΥψΚσ,œρ≤ΤΈώ¥ΠΆθάœ ΠΥΒ:ΓΑΈ“’β¥Έ¬ρ’βΝΫ÷÷± –η“Σ÷ßΝλ1322‘ΣΓ±Άθάœ ΠΚΥΥψΝΥ“Μœ¬,ΥΒ:ΓΑ»γΙϊΡψ”Ο’β–©«°÷Μ¬ρ’βΝΫ÷÷± ,Ρ«Ο¥’ΥΩœΕ®Υψ¥μΝΥ.Γ±«κΡψ”Ο―ßΙΐΒΡΖΫ≥Χ÷Σ ΕΫβ Ά:Άθάœ ΠΈΣ ≤Ο¥ΥΒ’≈άœ Π”Ο’β–©«°÷Μ¬ρΝΫ÷÷± ΒΡ’ΥΥψ¥μΝΥ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“Μ¥ΈΚ· ΐy=kx+b”κΖ¥±»άΐΚ· ΐy=![]() Θ®mΓΌ0Θ©ΒΡΆΦœσΫΜ”ΎΒψAΘ®3Θ§1Θ©Θ§«“ΙΐΒψBΘ®0Θ§©¹2Θ©Θ°
Θ®mΓΌ0Θ©ΒΡΆΦœσΫΜ”ΎΒψAΘ®3Θ§1Θ©Θ§«“ΙΐΒψBΘ®0Θ§©¹2Θ©Θ°
Θ®1Θ©«σΖ¥±»άΐΚ· ΐΚΆ“Μ¥ΈΚ· ΐΒΡ±μ¥ο ΫΘΜ
Θ®2Θ©»γΙϊΒψP «x÷α…œ“ΜΒψΘ§«“ΓςABPΒΡΟφΜΐ «3Θ§«σΒψPΒΡΉχ±ξΘ°
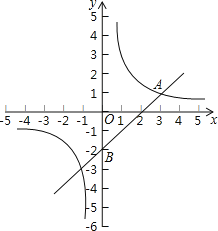
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ’ΐΖΫ–ΈABCD÷–Θ§E «Ε‘Ϋ«œΏBD…œ“ΜΒψΘ§«“¬ζΉψBEΘΫADΘ§Ν§Ϋ”CE≤Δ―”≥ΛΫΜAD”ΎΒψFΘ§Ν§Ϋ”AEΘ§ΙΐBΒψΉςBGΓΆAE”ΎΒψGΘ§―”≥ΛBGΫΜAD”ΎΒψHΘ°‘Ύœ¬Ν–Ϋα¬έ÷–ΘΚΔΌAHΘΫDFΘΜΔΎΓœAEFΘΫ45ΓψΘΜΔέSΥΡ±Ώ–ΈEFHGΘΫSΓςDEF+SΓςAGHΘΜΔήBHΤΫΖ÷ΓœABEΘ°Τδ÷–≤Μ’ΐ»ΖΒΡΫα¬έ”–Θ®ΓΓΓΓΘ©
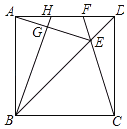
A. 1ΗωB. 2ΗωC. 3ΗωD. 4Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“ΜΑψΒΊΘ§»ΈΚΈ“ΜΗωΈόœό―≠ΜΖ–Γ ΐΕΦΩ…“‘–¥≥…Ζ÷ ΐ–Έ ΫΘ§»γ0.![]() ΘΫ0.777Γ≠Θ§ΥϋΒΡ―≠ΜΖΫΎ”–“ΜΈΜΘ§…η0.
ΘΫ0.777Γ≠Θ§ΥϋΒΡ―≠ΜΖΫΎ”–“ΜΈΜΘ§…η0. ![]() ΘΫxΘ§”…0.
ΘΫxΘ§”…0. ![]() ΘΫ0777Γ≠Θ§Ω…÷ΣΘ§10xΘΫ7.777Γ≠Θ§Υυ“‘10x©¹xΘΫ7Θ§ΒΟxΘΫ
ΘΫ0777Γ≠Θ§Ω…÷ΣΘ§10xΘΫ7.777Γ≠Θ§Υυ“‘10x©¹xΘΫ7Θ§ΒΟxΘΫ![]() Θ°”Ύ «Θ§ΒΟ0.
Θ°”Ύ «Θ§ΒΟ0. ![]() ΘΫ
ΘΫ![]() Θ§‘Ό»γ0.
Θ§‘Ό»γ0.![]() ΘΫ0.737373Γ≠Θ§ΥϋΒΡ―≠ΜΖΫΎ”–ΝΫΈΜΘ§…η0.
ΘΫ0.737373Γ≠Θ§ΥϋΒΡ―≠ΜΖΫΎ”–ΝΫΈΜΘ§…η0.![]() ΘΫxΘ§”…0.
ΘΫxΘ§”…0.![]() ΘΫ0.737373Γ≠Ω…÷ΣΘ§100xΘΫ73.7373Γ≠Θ§Υυ“‘100x©¹xΘΫ73Θ°ΫβΖΫ≥ΧΒΟxΘΫ
ΘΫ0.737373Γ≠Ω…÷ΣΘ§100xΘΫ73.7373Γ≠Θ§Υυ“‘100x©¹xΘΫ73Θ°ΫβΖΫ≥ΧΒΟxΘΫ![]() Θ°”Ύ «Θ§ΒΟ0.
Θ°”Ύ «Θ§ΒΟ0. ![]() ΘΫ
ΘΫ![]() Θ§άύ±»…œ ωΖΫΖ®Θ§Έόœό―≠ΜΖ–Γ ΐ0.
Θ§άύ±»…œ ωΖΫΖ®Θ§Έόœό―≠ΜΖ–Γ ΐ0. ![]() 3
3![]() Μ·ΈΣΖ÷ ΐ–Έ ΫΈΣ_____Θ°
Μ·ΈΣΖ÷ ΐ–Έ ΫΈΣ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΤλΗΥABΒΡΕΞΕΥB‘ΎœΠ―τΒΡ”ύΜ‘œ¬¬δ‘Ύ“ΜΗω–±Τ¬…œΒΡΒψD¥ΠΘ§Ρ≥–Θ ΐ―ßΩΈΆβ–Υ»Λ–ΓΉιΒΡΆ§―ß’ΐ‘Ύ≤βΝΩΤλΗΥΒΡΗΏΕ»Θ§‘ΎΤλΗΥΒΡΒΉ≤ΩA¥Π≤βΒΟΒψDΒΡ―ωΫ«ΈΣ15ΓψΘ§AC=10ΟΉΘ§”÷≤βΒΟΓœBDA=45ΓψΘ°“―÷Σ–±Τ¬CDΒΡΤ¬Ε»ΈΣi=1ΘΚ![]() Θ§«σΤλΗΥABΒΡΗΏΕ»Θ®
Θ§«σΤλΗΥABΒΡΗΏΕ»Θ®![]() Γ÷1.7Θ§ΫαΙϊΨΪ»ΖΒΫΗωΈΜΘ©Θ°
Γ÷1.7Θ§ΫαΙϊΨΪ»ΖΒΫΗωΈΜΘ©Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com