
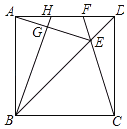
【题目】如图,在正方形ABCD中,E是对角线BD上一点,且满足BE=AD,连接CE并延长交AD于点F,连接AE,过B点作BG⊥AE于点G,延长BG交AD于点H.在下列结论中:①AH=DF;②∠AEF=45°;③S四边形EFHG=S△DEF+S△AGH;④BH平分∠ABE.其中不正确的结论有( )
A. 1个B. 2个C. 3个D. 4个
【答案】A
【解析】
先判断出∠DAE=∠ABH,再判断△ADE≌△CDE得出∠DAE=∠DCE=22.5°,∠ABH=∠DCF,再判断出Rt△ABH≌Rt△DCF从而得到①正确,根据三角形的外角求出∠AEF=45°,得出②正确;连接HE,判断出S△EFH≠S△EFD得出③错误,根据三角形的内角和和角平分线的定义得到④正确.
解:∵BD是正方形ABCD的对角线,
∴∠ABE=∠ADE=∠CDE=45°,AB=BC,
∵BE=BC,
∴AB=BE,
∵BG⊥AE,
∴BH是线段AE的垂直平分线,∠ABH=∠DBH=22.5°,
在Rt△ABH中,∠AHB=90°﹣∠ABH=67.5°,
∵∠AGH=90°,
∴∠DAE=∠ABH=22.5°,
在△ADE和△CDE中, ,
,
∴△ADE≌△CDE(SAS),
∴∠DAE=∠DCE=22.5°,
∴∠ABH=∠DCF,
在△ABH和△DCF中,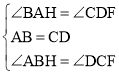 ,
,
∴△ABH≌△DCF(ASA),
∴AH=DF,∠CFD=∠AHB=67.5°,
∵∠CFD=∠EAF+∠AEF,
∴67.5°=22.5°+∠AEF,
∴∠AEF=45°,故①②正确;
如图,连接HE,
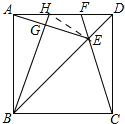
∵BH是AE垂直平分线,
∴AG=EG,
∴S△AGH=S△HEG,
∵AH=HE,
∴∠AHG=∠EHG=67.5°,
∴∠DHE=45°,
∵∠ADE=45°,
∴∠DEH=90°,∠DHE=∠HDE=45°,
∴EH=ED,
∴△DEH是等腰直角三角形,
∵EF不垂直DH,
∴FH≠FD,
∴S△EFH≠S△EFD,
∴S四边形EFHG=S△HEG+S△EFH=S△AHG+S△EFH≠S△DEF+S△AGH,故③错误,
∵∠AHG=67.5°,
∴∠ABH=22.5°,
∵∠ABD=45°,
∴∠ABH![]()
∴BH平分∠ABE,故④正确;
故选:A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°,将一直角三角板MON的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
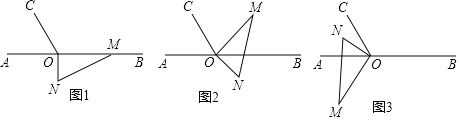
(1)求∠CON的度数;
(2)如图2是将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周的情况.在旋转的过程中,当第t秒时,三条射线OA、OC、OM构成相等的角,求此时t的值;
(3)将图1中的三角板绕点O逆时针旋转至图3,使ON在∠AOC的内部时,请探究∠AOM与∠CON的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小聪在复习过程中,发现数轴上线段的长度可以用线段端点表示的数进行减法运算得到,例:
如图1,线段![]() ,线段
,线段![]() ,
,

线段![]() ,线段
,线段![]()
结论:数轴上任意两点表示的数分别为:![]() ,
,![]() (
(![]() ),则这两点间的距离为:
),则这两点间的距离为:![]() (即:较大的数减去较小的数).
(即:较大的数减去较小的数).
尝试应用:
(1)若数轴上点![]() ,点
,点![]() 代表的数分别是-3,-1,则
代表的数分别是-3,-1,则![]() ______.
______.
(2)把一条数轴在数![]() 处对折,表示-9和3两数的点恰好互相重合,此时
处对折,表示-9和3两数的点恰好互相重合,此时![]() ______.
______.
(3)数轴上的两个点之间的距离为6,其中一个点表示的数为3,另一个点表示的数为![]() ,则
,则![]() ______.
______.
问题解决:
(4)如图2,点![]() 表示数
表示数![]() ,点
,点![]() 表示-2,点
表示-2,点![]() 表示
表示![]() 且
且![]() ,问点
,问点![]() 和点
和点![]() 分别表示什么数?为什么?
分别表示什么数?为什么?

(5)上述(4)的条件下,图2所示的数轴上,是否存在满足条件的点![]() ,使用
,使用![]() ?
?
若存在,请直接写出![]() 所表示的数,若不存在,请说明理由?(点
所表示的数,若不存在,请说明理由?(点![]() 不与点
不与点![]() ,点
,点![]() ,点
,点![]() 重合)
重合)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC、BD相交于点O,点P是线段AD上一动点(不与与点D重合),PO的延长线交BC于Q点.
(1)求证:四边形PBQD为平行四边形.
(2)若AB=6cm,AD=8cm,P从点A出发.以1cm/秒的速度向点D匀速运动.设点P运动时间为t秒,问四边形PBQD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )
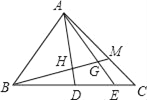
A. 3:2:1 B. 5:3:1 C. 25:12:5 D. 51:24:10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线![]() 与坐标轴交于A,B两点,以AB为斜边在第一象限内作等腰直角三角形ABC,点C为直角顶点,连接OC.
与坐标轴交于A,B两点,以AB为斜边在第一象限内作等腰直角三角形ABC,点C为直角顶点,连接OC.
(1)直接写出![]() = ;
= ;
(2)请你过点C作CE⊥y轴于E点,试探究OB+OA与CE的数量关系,并证明你的结论;
(3)若点M为AB的中点,点N为OC的中点,求MN的值;
(4)如图2,将线段AB绕点B沿顺时针方向旋转至BD,且OD⊥AD,延长DO交直线![]() 于点P,求点P的坐标.
于点P,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
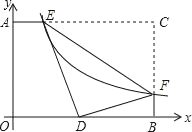
【题目】如图,在矩形AOBC中,OB=4,OA=3,分别以OB,OA所在直线为x轴、y轴建立平面直角坐标系,F是BC边上的点,过F点的反比例函数y=![]() (k>0)的图象与AC边交于点E.若将△CEF沿EF翻折后,点C恰好落在OB上的点D处,则点F的坐标为_____.
(k>0)的图象与AC边交于点E.若将△CEF沿EF翻折后,点C恰好落在OB上的点D处,则点F的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西安某学校为了改善办学条件,计划购置一批电子白板和台式电脑.经招投标,购买一台电子白板比购买2台台式电脑多3000元,购买2台电子白板和3台台式电脑共需2.7万元.
(1)设购买一台台式电脑需![]() 元,购买一台电子白板需 元(用含
元,购买一台电子白板需 元(用含![]() 的代数式表示)
的代数式表示)
(2)求购买一台电子白板和一台台式电脑各需多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com