
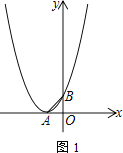
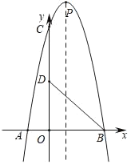
【题目】已知抛物线顶点![]() 在
在![]() 轴负半轴上,与
轴负半轴上,与![]() 轴交于点
轴交于点![]() ,
,![]() ,
,![]() 为等腰直角三角形.
为等腰直角三角形.
(1)求抛物线的解析式
(2)若点![]() 在抛物线上,若
在抛物线上,若![]() 为直角三角形,求点
为直角三角形,求点![]() 的坐标
的坐标
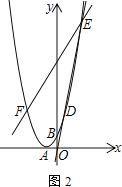
(3)已知直线![]() 过点
过点![]() ,交抛物线于点
,交抛物线于点![]() 、
、![]() ,过
,过![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,求证:直线
,求证:直线![]() 经过一个定点,并求定点的坐标.
经过一个定点,并求定点的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)(-1,4)
;(3)(-1,4)
【解析】
(1)先求出顶点坐标与y轴交点坐标,根据顶点式求二次函数解析式;
(2)根据直角三角形的判定定理找出△ABC为直角三角形,分三种情况:当A为直角顶点时,AC⊥AB;当B为直角顶点时,BC⊥AB;当C为直角顶点,分别确定点C的坐标;
(3)根据二次函数与方程的关系求解.
(1)∵OB=1,点B在y轴的正半轴上,
∴B(0,1),
∵△OAB为等腰直角三角形,
∴OA=OB=1,
∵顶点A在x轴负半轴上,
∴顶点A(-1,0),
∴设y=a(x+1)2,
把B(0,1)代入得
1=a×(0+1)2,
∴a=1,
∴![]() ,
,
(2)当A为直角顶点时,AC⊥AB,
设直线AB解析式为y=mx+n,
∵B(0,1),A(-1,0),
∴![]() ,
,
∴![]() ,
,
∴直线AB解析式为y=x+1,
∵AC⊥AB,
∴直线AC解析式为y=-x-1,
联立得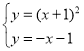 ,
,
解得: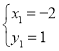 ,
,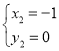 ,
,
∴C(-2,1).
当B为直角顶点时,BC⊥AB,
∵直线AB解析式为y=x+1,
∴直线BC解析式为y=-x+1,
同理可得C(-3,4),
当C为直角顶点不存在 .
综上所述点C坐标为(-2,1)或(-3,4),
(3)设DE的解析式为![]() ,
,
联立![]() ,
,
∴![]() ,
,
得: ,
,
∵D,E关于对称轴对称,
所以![]() ,
,
设EF的解析式为![]() 联立,
联立,
![]() ,
,
得![]() ,
,
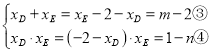 ,
,
联立①②③④得n=m+4,
所以![]() ,过定点(-1,4),
,过定点(-1,4),
即直线EF经过一个定点,定点的坐标为(-1,4).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
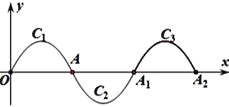
【题目】如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1 ,它与x轴交于两点O,A;将C1绕点A旋转180°得到C2 , 交x轴于A1;将C2绕点A1旋转180°得到C3 , 交x轴于点A2 . .....如此进行下去,直至得到C2018 , 若点P(4035,m)在第2018段抛物线上,则m的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
(1)请直接写出D点的坐标.
(2)求二次函数的解析式.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:有一内角为直角的三角形叫做直角三角形.类似地我们定义:有一内角为45°的三角形叫做半直角三角形.如图,在平面直角坐标系中,O为原点,A(4,0),B(-4,0),D是y轴上的一个动点,∠ADC=90°(A、D、C按顺时针方向排列), BC与经过A、B、D三点的⊙M交于点E,DE平分∠ADC,连结AE,BD.显然ΔDCE、ΔDEF、ΔDAE是半直角三角形.
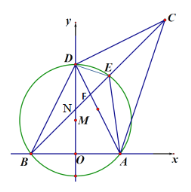
(1)求证:ΔABC是半直角三角形;
(2)求证:∠DEC=∠DEA;
(3)若点D的坐标为(0,8),求AE的长;
(4)BC交y轴于点N,问![]() 的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+8与x轴相交于点A(﹣2,0)和点B(4,0),与y轴相交于点C,顶点为点P.点D(0,4)在OC上,联结BC、BD.
(1)求抛物线的表达式并直接写出点P的坐标;
(2)点E为第一象限内抛物线上一点,如果△COE与△BCD的面积相等,求点E的坐标;
(3)点Q在抛物线对称轴上,如果△BCD∽△CPQ,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经过市场调查,整理出某种商品在第x(x≤90)天的售价与销量的相关信息如右表.已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元件) | x+40 | 90 |
每天销量(件) | 200-2x | |
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在的圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰△ABC中,AB=AC,将线段BA绕点B顺时针旋转到BD,使BD⊥AC于H,连结AD并延长交BC的延长线于点P.
(1)依题意补全图形;
(2)若∠BAC=2α,求∠BDA的大小(用含α的式子表示);
(3)小明作了点D关于直线BC的对称点点E,从而用等式表示线段DP与BC之间的数量关系.请你用小明的思路补全图形并证明线段DP与BC之间的数量关系.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com