
【题目】某商店经过市场调查,整理出某种商品在第x(x≤90)天的售价与销量的相关信息如右表.已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元件) | x+40 | 90 |
每天销量(件) | 200-2x | |
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
【答案】(1)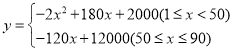 ;(2)商品第45天时,当天销售利润最大,最大利润是6050元.
;(2)商品第45天时,当天销售利润最大,最大利润是6050元.
【解析】
(1)分成1≤x<50和50≤x≤90两种情况进行讨论,利用:利润=每件的利润×销售的件数,即可求得函数的解析式;
(2)结合(1)得到的两个解析式,结合二次函数与一次函数的性质分别求得最值,然后两种情况下取最大的即可.
解:(1)当1≤x<50时,y=(200-2x)(x+40-30)
=-2x2+180x+2000
=-(x-45)2+6050,
当50≤x≤90时,
y=(200-2x)(90-30)=-120x+12000,
综上所述: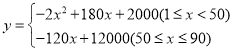 ;
;
(2)当1≤x<50时,二次函数开口下,二次函数对称轴为x=45,
当x=45时,y最大=6050,
当50≤x≤90时,y随x的增大而减小,
当x=50时,y最大=6000,
综上所述,该商品第45天时,当天销售利润最大,最大利润是6050元.


科目:初中数学 来源: 题型:
【题目】端午节那天,小贤回家看到桌上有一盘粽子,其中有豆沙粽、肉粽各1个,蜜枣粽2个,这些粽子除馅外无其他差别.
(1)小贤随机地从盘中取出一个粽子,取出的是肉粽的概率是多少?
(2)小贤随机地从盘中取出两个粽子,试用画树状图或列表的方法表示所有可能的结果,并求出小贤取出蜜枣粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
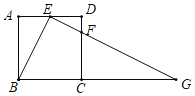
【题目】如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且∠BEF=90°,延长EF交BC的延长线于点G.
(1)求证:△ABE∽△EGB.
(2)若AB=4,求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
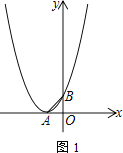
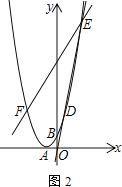
【题目】已知抛物线顶点![]() 在
在![]() 轴负半轴上,与
轴负半轴上,与![]() 轴交于点
轴交于点![]() ,
,![]() ,
,![]() 为等腰直角三角形.
为等腰直角三角形.
(1)求抛物线的解析式
(2)若点![]() 在抛物线上,若
在抛物线上,若![]() 为直角三角形,求点
为直角三角形,求点![]() 的坐标
的坐标
(3)已知直线![]() 过点
过点![]() ,交抛物线于点
,交抛物线于点![]() 、
、![]() ,过
,过![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,求证:直线
,求证:直线![]() 经过一个定点,并求定点的坐标.
经过一个定点,并求定点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把抛物线![]() 先向左平移
先向左平移![]() 个单位长度,再向上平移
个单位长度,再向上平移![]() 个单位长度,得到抛物线
个单位长度,得到抛物线![]() .
.
(1)试确定![]() 的值;
的值;
(2)作原抛物线关于![]() 轴对称的图形,求所得抛物线的函数表达式.
轴对称的图形,求所得抛物线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
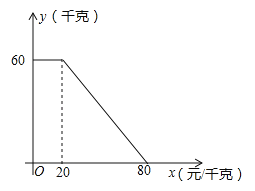
【题目】某商店以20元/千克的单价新进一批商品,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间为一次函数关系,如图所示.
(1)求y与x的函数表达式;
(2)要使销售利润达到800元,销售单价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
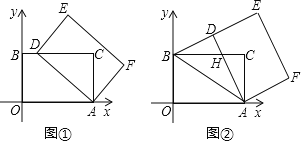
【题目】在平面直角坐标系中,四边形AOBC是矩形,点O(0,0),点A(5,0),点B(0,3).以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,点O,B,C的对应点分别为D,E,F.
(1)如图①,当点D落在BC边上时,求点D的坐标;
(2)如图②,当点D落在线段BE上时,AD与BC交于点H.
①求证△ADB≌△AOB;
②求点H的坐标.
(3)记K为矩形AOBC对角线的交点,S为△KDE的面积,求S的取值范围(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解市民对全市创文工作的满意程度,某中学数学兴趣小组在全市甲、乙两个区内进行了调查统计,将调查结果分为不满意,一般,满意,非常满意四类,回收、整理好全部问卷后,得到下列不完整的统计图.
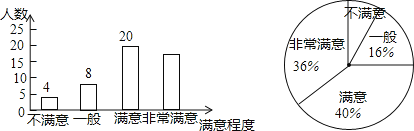
请结合图中信息,解决下列问题:
(1)求此次调查中接受调查的人数.
(2)求此次调查中结果为非常满意的人数.
(3)兴趣小组准备从调查结果为不满意的4位市民中随机选择2位进行回访,已知4位市民中有2位来自甲区,另2位来自乙区,请用列表或用画树状图的方法求出选择的市民均来自甲区的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com