
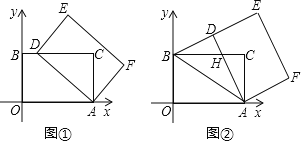
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЫФБпаЮAOBCЪЧОиаЮЃЌЕуOЃЈ0ЃЌ0ЃЉЃЌЕуAЃЈ5ЃЌ0ЃЉЃЌЕуBЃЈ0ЃЌ3ЃЉЃЎвдЕуAЮЊжааФЃЌЫГЪБеыа§зЊОиаЮAOBCЃЌЕУЕНОиаЮADEFЃЌЕуOЃЌBЃЌCЕФЖдгІЕуЗжБ№ЮЊDЃЌEЃЌFЃЎ
ЃЈ1ЃЉШчЭМЂйЃЌЕБЕуDТфдкBCБпЩЯЪБЃЌЧѓЕуDЕФзјБъЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌЕБЕуDТфдкЯпЖЮBEЩЯЪБЃЌADгыBCНЛгкЕуHЃЎ
ЂйЧѓжЄЁїADBЁеЁїAOBЃЛ
ЂкЧѓЕуHЕФзјБъЃЎ
ЃЈ3ЃЉМЧKЮЊОиаЮAOBCЖдНЧЯпЕФНЛЕуЃЌSЮЊЁїKDEЕФУцЛ§ЃЌЧѓSЕФШЁжЕЗЖЮЇЃЈжБНгаДГіНсЙћМДПЩЃЉЃЎ
ЁОД№АИЁПЃЈ1ЃЉDЃЈ1ЃЌ3ЃЉЃЛЃЈ2ЃЉЂйЯъМћНтЮіЃЛЂкHЃЈ![]() ЃЌ3ЃЉЃЛЃЈ3ЃЉ
ЃЌ3ЃЉЃЛЃЈ3ЃЉ![]() ЁмSЁм
ЁмSЁм![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМЂйЃЌдкRtЁїACDжаЧѓГіCDМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉЂйИљОнHLжЄУїМДПЩЃЛ
ЂкЃЌЩшAH=BH=mЃЌдђHC=BC-BH=5-mЃЌдкRtЁїAHCжаЃЌИљОнAH2=HC2+AC2ЃЌЙЙНЈЗНГЬЧѓГіmМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉШчЭМЂлжаЃЌЕБЕуDдкЯпЖЮBKЩЯЪБЃЌЁїDEKЕФУцЛ§зюаЁЃЌЕБЕуDдкBAЕФбгГЄЯпЩЯЪБЃЌЁїDЁфEЁфKЕФУцЛ§зюДѓЃЌЧѓГіУцЛ§ЕФзюаЁжЕвдМАзюДѓжЕМДПЩНтОіЮЪЬтЃЛ
ЃЈ1ЃЉШчЭМЂйжаЃЌ
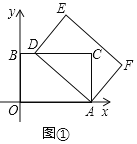
ЁпAЃЈ5ЃЌ0ЃЉЃЌBЃЈ0ЃЌ3ЃЉЃЌ
ЁрOA=5ЃЌOB=3ЃЌ
ЁпЫФБпаЮAOBCЪЧОиаЮЃЌ
ЁрAC=OB=3ЃЌOA=BC=5ЃЌЁЯOBC=ЁЯC=90ЁуЃЌ
ЁпОиаЮADEFЪЧгЩОиаЮAOBCа§зЊЕУЕНЃЌ
ЁрAD=AO=5ЃЌ
дкRtЁїADCжаЃЌCD=![]() =4ЃЌ
=4ЃЌ
ЁрBD=BC-CD=1ЃЌ
ЁрDЃЈ1ЃЌ3ЃЉЃЎ
ЃЈ2ЃЉЂйШчЭМЂкжаЃЌ
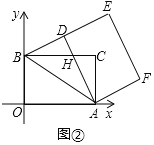
гЩЫФБпаЮADEFЪЧОиаЮЃЌЕУЕНЁЯADE=90ЁуЃЌ
ЁпЕуDдкЯпЖЮBEЩЯЃЌ
ЁрЁЯADB=90ЁуЃЌ
гЩЃЈ1ЃЉПЩжЊЃЌAD=AOЃЌгжAB=ABЃЌЁЯAOB=90ЁуЃЌ
ЁрRtЁїADBЁеRtЁїAOBЃЈHLЃЉЃЎ
ЂкШчЭМЂкжаЃЌгЩЁїADBЁеЁїAOBЃЌЕУЕНЁЯBAD=ЁЯBAOЃЌ
гждкОиаЮAOBCжаЃЌOAЁЮBCЃЌ
ЁрЁЯCBA=ЁЯOABЃЌ
ЁрЁЯBAD=ЁЯCBAЃЌ
ЁрBH=AHЃЌЩшAH=BH=mЃЌдђHC=BC-BH=5-mЃЌ
дкRtЁїAHCжаЃЌЁпAH2=HC2+AC2ЃЌ
Ёрm2=32+ЃЈ5-mЃЉ2ЃЌ
Ёрm=![]() ЃЌ
ЃЌ
ЁрBH=![]() ЃЌ
ЃЌ
ЁрHЃЈ![]() ЃЌ3ЃЉЃЎ
ЃЌ3ЃЉЃЎ
ЃЈ3ЃЉШчЭМЂлжаЃЌЕБЕуDдкЯпЖЮBKЩЯЪБЃЌЁїDEKЕФУцЛ§зюаЁЃЌзюаЁжЕ=![]() DEDK=
DEDK=![]() ЁС3ЁСЃЈ5-
ЁС3ЁСЃЈ5-![]() ЃЉ=
ЃЉ=![]() ЃЌ
ЃЌ
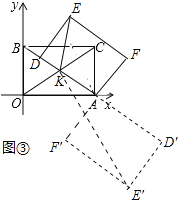
ЕБЕуDдкBAЕФбгГЄЯпЩЯЪБЃЌЁїDЁфEЁфKЕФУцЛ§зюДѓЃЌзюДѓУцЛ§=![]() ЁСDЁфEЁфЁСKDЁф=
ЁСDЁфEЁфЁСKDЁф=![]() ЁС3ЁСЃЈ5+
ЁС3ЁСЃЈ5+![]() ЃЉ=
ЃЉ=![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃЌ![]() ЁмSЁм
ЁмSЁм![]() ЃЎ
ЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
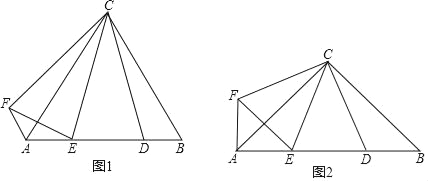
ЁОЬтФПЁПЃЈ1ЃЉВйОПЗЂЯжЃКШчЭМ1ЃЌЁїABCЮЊЕШБпШ§НЧаЮЃЌЕуDЮЊABБпЩЯЕФвЛЕуЃЌЁЯDCE=30ЁуЃЌЁЯDCF=60ЁуЧвCF=CD
ЂйЧѓЁЯEAFЕФЖШЪ§ЃЛ
ЂкDEгыEFЯрЕШТ№ЃПЧыЫЕУїРэгЩ
ЃЈ2ЃЉРрБШЬНОПЃКШчЭМ2ЃЌЁїABCЮЊЕШбќжБНЧШ§НЧаЮЃЌЁЯACB=90ЁуЃЌЕуDЮЊABБпЩЯЕФвЛЕуЃЌЁЯDCE=45ЁуЃЌCF=CDЃЌCFЁЭCDЃЌЧыжБНгаДГіЯТСаНсЙћЃК
ЂйЁЯEAFЕФЖШЪ§
ЂкЯпЖЮAEЃЌEDЃЌDBжЎМфЕФЪ§СПЙиЯЕ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
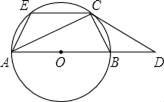
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌCЪЧЁбOЩЯвЛЕуЃЌЙ§CЕуЕФЧаЯпгыABЕФбгГЄЯпНЛгкЕуDЃЌCEЁЮABНЛЁбOгкЕуEЃЌСЌНгACЁЂBCЁЂAEЃЎ
ЃЈ1ЃЉЧѓжЄЃКЂйЁЯDCB=ЁЯCABЃЛЂкCDCE=CBCAЃЛ
ЃЈ2ЃЉзїCGЁЭABгкЕуGЃЎШєtanЁЯCABЃН![]() ЃЈkЃО1ЃЉЃЌЧѓ
ЃЈkЃО1ЃЉЃЌЧѓ![]() ЕФжЕЃЈгУКЌkЕФЪНзгБэЪОЃЉЃЎ
ЕФжЕЃЈгУКЌkЕФЪНзгБэЪОЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПе§ЗНаЮA1B1C1OЃЌе§ЗНаЮA2B2C2C1ЃЌе§ЗНаЮA3B3C3C2ЃЌАДШчЭМЫљЪОЕФЗНЪНЗХжУдкЦНУцжБНЧзјБъЯЕжаЃЌШєЕуA1ЁЂA2ЁЂA3КЭC1ЁЂC2ЁЂC3ЁЗжБ№дкжБЯпyЃНx+1КЭxжсЩЯЃЌдђЕуB2019ЕФзјБъЪЧ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§yЃНЉx+4ЕФЭМЯѓгыЗДБШР§КЏЪ§yЃН![]() ЃЈkЁй0ЃЉЕФЭМЯѓНЛгкAЃЈ1ЃЌaЃЉЁЂBЃЈbЃЌ1ЃЉСНЕуЃЎ
ЃЈkЁй0ЃЉЕФЭМЯѓНЛгкAЃЈ1ЃЌaЃЉЁЂBЃЈbЃЌ1ЃЉСНЕуЃЎ
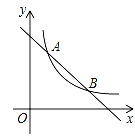
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉдкxжсЩЯеввЛЕуPЃЌЪЙPA+PBЕФжЕзюаЁЃЌЧѓТњзуЬѕМўЕФЕуPЕФзјБъЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЧѓЁїPABЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁРћЭЌбЇЕїВщСЫШЋАр50УћЭЌбЇЗжБ№ЯВЛЖЯрЩљЁЂаЁЦЗЁЂИшЧњЁЂЮшЕИНкФПЕФЧщПіЃЌВЂжЦГЩЯТУцЕФЭГМЦБэЃК
зюЯВЛЖЕФНкФПЕФРрБ№ | ЛЎМЧ | ШЫЪ§ | АйЗжБШЃЈ%ЃЉ |
ЯрЩљ | е§ | 9 | 12 |
аЁЦЗ | е§е§е§ | 21 | 42 |
ИшЧњ | е§е§ | 10 | 28 |
ЮшЕИ | е§ | 6 | 12 |
дкБэжаЕФЪ§ОнжаЃЌНігавЛРрНкФПЕФЭГМЦЪЧЭъШЋе§ШЗЕФЃЌдђИУЯюЭГМЦРрБ№ЪЧЃЈ ЃЉ
A. ЯрЩљB. ЮшЕИC. ИшЧњD. аЁЦЗ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћЕуAЃЈ0ЃЌ2ЃЉКЭЕуBЃЈ4ЃЌ2ЃЉЖМдкЖўДЮКЏЪ§y=x2+bx+cЕФЭМЯѓЩЯЃЌФЧУДДЫХзЮяЯпдкжБЯп_____ЕФВПЗжЪЧЩЯЩ§ЕФЃЎЃЈЬюОпЬхФГжБЯпЕФФГВрЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшaЃЌbЪЧШЮвтСНИіВЛЕШЪЕЪ§ЃЌЮвУЧЙцЖЈЃКТњзуВЛЕШЪНaЁмxЁмbЕФЪЕЪ§xЕФЫљгаШЁжЕЕФШЋЬхНазіБеЧјМфЃЌБэЪОЮЊ[aЃЌb]ЃЎЖдгквЛИіКЏЪ§ЃЌШчЙћЫќЕФздБфСПxгыКЏЪ§жЕyТњзуЃКЕБmЁмxЁмnЪБЃЌгаmЁмyЁмnЃЌЮвУЧОЭГЦДЫКЏЪ§ЪЧБеЧјМф[mЃЌn]ЩЯЕФЁАБеКЏЪ§ЁБЃЎШчКЏЪ§y=Љx+4ЃЌЕБx=1ЪБЃЌy=3ЃЛЕБx=3ЪБЃЌy=1ЃЌМДЕБ1ЁмxЁм3ЪБЃЌКуга1ЁмyЁм3ЃЌЫљвдЫЕКЏЪ§y=Љx+4ЪЧБеЧјМф[1ЃЌ3]ЩЯЕФЁАБеКЏЪ§ЁБЃЌЭЌРэКЏЪ§y=xвВЪЧБеЧјМф[1ЃЌ3]ЩЯЕФЁАБеКЏЪ§ЁБЃЎ
ЃЈ1ЃЉЗДБШР§КЏЪ§y=![]() ЪЧБеЧјМф[1ЃЌ2018]ЩЯЕФЁАБеКЏЪ§ЁБТ№ЃПЧыХаЖЯВЂЫЕУїРэгЩЃЛ
ЪЧБеЧјМф[1ЃЌ2018]ЩЯЕФЁАБеКЏЪ§ЁБТ№ЃПЧыХаЖЯВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШчЙћвбжЊЖўДЮКЏЪ§y=x2Љ4x+kЪЧБеЧјМф[2ЃЌt]ЩЯЕФЁАБеКЏЪ§ЁБЃЌЧѓkКЭtЕФжЕЃЛ
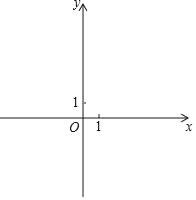
ЃЈ3ЃЉШчЙћЃЈ2ЃЉЫљЪіЕФЖўДЮКЏЪ§ЕФЭМЯѓНЛyжсгкCЕуЃЌAЮЊДЫЖўДЮКЏЪ§ЭМЯѓЕФЖЅЕуЃЌBЮЊжБЯпx=1ЩЯЕФвЛЕуЃЌЕБЁїABCЮЊжБНЧШ§НЧаЮЪБЃЌаДГіЕуBЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФПЧАНкФмЕЦдкГЧЪавбЛљБОЦеМАЃЌФГЩЬГЁМЦЛЎЙКНјМзЁЂввСНжжНкФмЖЉЙВ1200жЛЃЌетСНжжНкФмЕЦЕФНјМлЁЂЪлМлШчЯТБэЃК
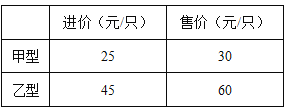
ЃЈ1ЃЉШчКЮНјЛѕЃЌНјЛѕПюЧЁКУЮЊ46000дЊ?
ЃЈ2ЃЉЮЊШЗБЃвваЭНкФмЕЦЫГРћГЉЯњЃЌдкЃЈ1ЃЉЕФЬѕМўЯТЃЌЩЬМвОіЖЈЖдвваЭНкФмЕЦНјааДђелГіЪлЃЌЧвШЋВПЪлЭъКѓЃЌвваЭНкФмЕЦЕФРћШѓТЪЮЊ20%ЃЌЧыЭЌвваЭНкФмЕЦашДђМИел?
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com