
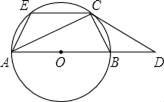
【题目】已知:如图,AB是⊙O的直径,C是⊙O上一点,过C点的切线与AB的延长线交于点D,CE∥AB交⊙O于点E,连接AC、BC、AE.
(1)求证:①∠DCB=∠CAB;②CDCE=CBCA;
(2)作CG⊥AB于点G.若tan∠CAB=![]() (k>1),求
(k>1),求![]() 的值(用含k的式子表示).
的值(用含k的式子表示).
【答案】(1)见解析;(2)![]()
【解析】分析:(1)①过点C作直径CF,连接BF.即可得![]() 又由直径所对的圆周角等于直角,可得
又由直径所对的圆周角等于直角,可得![]() 又由切线的性质,可得
又由切线的性质,可得![]() 是直角,即可证得
是直角,即可证得![]() ②由EC∥AB,易证得∠4=∠3=∠BCD.有圆的内接四边形的对角互补,可得∠CBD=∠AEC.即可证得
②由EC∥AB,易证得∠4=∠3=∠BCD.有圆的内接四边形的对角互补,可得∠CBD=∠AEC.即可证得![]() 则得到
则得到![]()
(2)在![]() 与
与![]() 中,利用三角函数的性质,即可求得
中,利用三角函数的性质,即可求得![]() 的值.
的值.
详解:(1)证明:①如图1,
作直径CF,连接BF.
∴![]()
则![]()
∵CD切![]() 于C,
于C,
∴OC⊥CD,
则![]()
∴∠BCD=∠CAB.
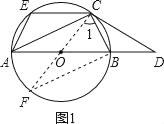
②∵EC∥AB,∠BCD=∠3,
∴∠4=∠3=∠BCD.
∵![]()
∵![]()
∴∠CBD=∠AEC.
∴△ACE∽△DCB.
∴![]()
∴CDCE=CBCA.
(2)如图2,连接EB,交OC于点H,
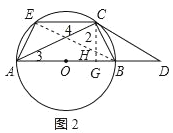
∵CG⊥AB于点G,![]()
∴∠3=∠BCG.
∴AE=BC,
∵∠3=∠4.
∴∠3=∠EBG.
∴∠BCG=∠EBG.
∵![]()
∴在Rt△HGB中,![]()
在Rt△BCG中,![]()
设HG=a,则![]()
∵EC∥AB,
∴△ECH∽△BGH.
∴![]()


科目:初中数学 来源: 题型:
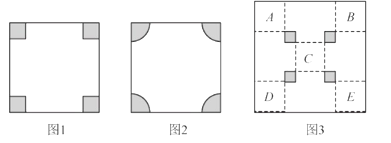
【题目】(1)探索:如图1,在边长为![]() 的正方形纸片的4个角都剪去1个边长是
的正方形纸片的4个角都剪去1个边长是![]() 的正方形.试用含
的正方形.试用含![]() 的式子表示纸片剩余部分的面积为_______________________;
的式子表示纸片剩余部分的面积为_______________________;
(2)变式:如图2,在边长为![]() 的正方形纸片的4个角都剪去一个相同的扇形,扇形的半径为
的正方形纸片的4个角都剪去一个相同的扇形,扇形的半径为![]() ,用
,用![]() 表示纸片剩余部分面积为______________________,剩余部分图形的周长为_____________________;
表示纸片剩余部分面积为______________________,剩余部分图形的周长为_____________________;
(3)拓展:世博会中国国家馆模型的平面图如图3所示,其外框是一个大正方形,中间四个全等的小正方形(阴影部分)是支撑展馆的核心筒,标记字母的五个全等的正方形是展厅,展厅的边长为![]() ,已知核心筒的边长比展厅的边长的一半多1米,用含有
,已知核心筒的边长比展厅的边长的一半多1米,用含有![]() 的式子表示外框的边长
的式子表示外框的边长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备进一批季节性小家电,每个进价为40元,经市场预测,销售定价为50元,可售出400个;定价每增加1元,销售量将减少10个.设每个定价增加x元.
(1)写出售出一个可获得的利润是多少元(用含x的代数式表示)?
(2)商店若准备获得利润6000元,并且使进货量较少,则每个定价为多少元?应进货多少个?
(3)商店若要获得最大利润,则每个应定价多少元?获得的最大利润是多少?
【答案】(1)x+10元;(2)每个定价为70元,应进货200个.(3)每个定价为65元时得最大利润,可获得的最大利润是6250元.
【解析】试题分析:(1)根据利润=销售价-进价列关系式,(2)总利润=每个的利润×销售量,销售量为400-10x,列方程求解,根据题意取舍,(3)利用函数的性质求最值.
试题解析:由题意得:(1)50+x-40=x+10(元),
(2)设每个定价增加x元,
列出方程为:(x+10)(400-10x)=6000,解得:x1=10,x2=20,要使进货量较少,则每个定价为70元,应进货200个,
(3)设每个定价增加x元,获得利润为y元,
y=(x+10)(400-10x)=-10x2+300x+4000=-10(x-15)2+6250,当x=15时,y有最大值为6250,所以每个定价为65元时得最大利润,可获得的最大利润是6250元.
【题型】解答题
【结束】
24
【题目】猜想与证明:
如图1,摆放矩形纸片ABCD与矩形纸片ECGF,使B、C、G三点在一条直线上,CE在边CD上,连接AF,若M为AF的中点,连接DM、ME,试猜想DM与ME的关系,并证明你的结论.
拓展与延伸:
(1)若将”猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为 .
(2)如图2摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市提倡“诵读中华经典,营造书香校园”的良好诵读氛围,促进校园文化建设,进而培养学生的良好诵读习惯,使经典之风浸漫校园.某中学为了了解学生每周在校经典诵读时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) | 频数(人数) | 频率 |
2≤t<3 | 4 | 0.1 |
3≤t<4 | 10 | 0.25 |
4≤t<5 | a | 0.15 |
5≤t<6 | 8 | b |
6≤t<7 | 12 | 0.3 |
合计 | 40 | 1 |
(1)表中的a= ,b= ;
(2)请将频数分布直方图补全;
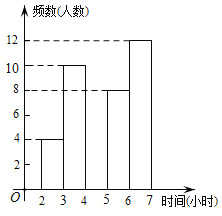
(3)若该校共有1200名学生,试估计全校每周在校参加经典诵读时间至少有4小时的学生约为多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A、B、C、D四个点,分别对应的数为a,b,c,d,且满足a,b是方程|x+7|=1的两个解(a<b),且(c﹣12)2与|d﹣16|互为相反数.
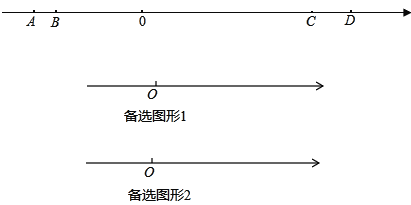
(1)填空:a= 、b= 、c= 、d= ;
(2)若线段AB以3个单位/秒的速度向右匀速运动,同时线段CD以1单位长度/秒向左匀速运动,并设运动时间为t秒,A、B两点都运动在CD上(不与C,D两个端点重合),若BD=2AC,求t得值;
(3)在(2)的条件下,线段AB,线段CD继续运动,当点B运动到点D的右侧时,问是否存在时间t,使BC=3AD?若存在,求t得值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
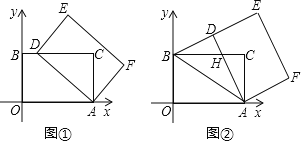
【题目】在平面直角坐标系中,四边形AOBC是矩形,点O(0,0),点A(5,0),点B(0,3).以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,点O,B,C的对应点分别为D,E,F.
(1)如图①,当点D落在BC边上时,求点D的坐标;
(2)如图②,当点D落在线段BE上时,AD与BC交于点H.
①求证△ADB≌△AOB;
②求点H的坐标.
(3)记K为矩形AOBC对角线的交点,S为△KDE的面积,求S的取值范围(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
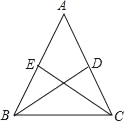
【题目】如图,等腰三角形ABC中,BD,CE分别是两腰上的中线.
(1)求证:BD=CE;
(2)设BD与CE相交于点O,点M,N分别为线段BO和CO的中点,当△ABC的重心到顶点A的距离与底边长相等时,判断四边形DEMN的形状,无需说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com