
【题目】如图,在数轴上有A、B、C、D四个点,分别对应的数为a,b,c,d,且满足a,b是方程|x+7|=1的两个解(a<b),且(c﹣12)2与|d﹣16|互为相反数.
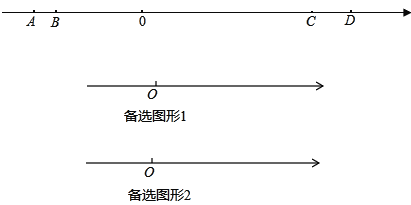
(1)填空:a= 、b= 、c= 、d= ;
(2)若线段AB以3个单位/秒的速度向右匀速运动,同时线段CD以1单位长度/秒向左匀速运动,并设运动时间为t秒,A、B两点都运动在CD上(不与C,D两个端点重合),若BD=2AC,求t得值;
(3)在(2)的条件下,线段AB,线段CD继续运动,当点B运动到点D的右侧时,问是否存在时间t,使BC=3AD?若存在,求t得值;若不存在,说明理由.
【答案】(1)﹣8;﹣6;12;16(2)t=![]() (3)t=
(3)t=![]() 或t=
或t=![]() 时,BC=3AD
时,BC=3AD
【解析】
(1)根据方程与非负数的性质即可求出答案.
(2)AB、CD运动时,点A对应的数为:﹣8+3t,点B对应的数为:﹣6+3t,点C对应的数为:12﹣t,点D对应的数为:16﹣t,根据题意列出等式即可求出t的值.
(3)根据题意求出t的范围,然后根据BC=3AD求出t的值即可.
(1)∵|x+7|=1,
∴x=﹣8或﹣6
∴a=﹣8,b=﹣6,
∵(c﹣12)2+|d﹣16|=0,
∴c=12,d=16,
(2)AB、CD运动时,
点A对应的数为:﹣8+3t,
点B对应的数为:﹣6+3t,
点C对应的数为:12﹣t,
点D对应的数为:16﹣t,
∴BD=|16﹣t﹣(﹣6+3t)|=|22﹣4t|
AC=|12﹣t﹣(﹣8+3t)|=|20﹣4t|
∵BD=2AC,
∴22﹣4t=±2(20﹣4t)
解得:t=![]() 或t=
或t=![]()
当t=![]() 时,此时点B对应的数为
时,此时点B对应的数为![]() ,点C对应的数为
,点C对应的数为![]() ,此时不满足题意,
,此时不满足题意,
故t=![]()
(3)当点B运动到点D的右侧时,
此时﹣6+3t>16﹣t
∴t>![]() ,
,
BC=|12﹣t﹣(﹣6+3t)|=|18﹣4t|,
AD=|16﹣t﹣(﹣8+3t)|=|24﹣4t|,
∵BC=3AD,
∴|18﹣4t|=3|24﹣4t|,
解得:t=![]() 或t=
或t=![]()
经验证,t=![]() 或t=
或t=![]() 时,BC=3AD
时,BC=3AD


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
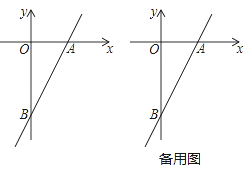
【题目】已知一次函数y=2x﹣4的图象与x轴、y轴分别相交于点A,B,点P在该函数图象上,P到x轴、y轴的距离分别为d1,d2.
(1)当P为线段AB的中点时,d1+d2=_____;
(2)设点P横坐标为m,用含m的代数式表示d1+d2,并求当d1+d2=3时点P的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE交BD于G,交BC于H,下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=![]() (∠BAC﹣∠C);④∠BGH=∠ABE+∠C.
(∠BAC﹣∠C);④∠BGH=∠ABE+∠C.
其中正确的是( )

A. ①②③ B. ①③④ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三位数,其个位数加上十位数等于百位数,可表示为t=100(x+y)+10y+x,则称实数t为“加成数”,将t的百位作为个位,个位作为十位,十位作为百位,组成一个新的三位数h.规定q=t﹣h,f(m)=![]() ,例如:321是一个“加成数”,将其百位作为个位,个位作为十位,十位作为百位,得到的数h=213,∴q=321﹣213=108,f(m)=
,例如:321是一个“加成数”,将其百位作为个位,个位作为十位,十位作为百位,得到的数h=213,∴q=321﹣213=108,f(m)=![]() =12.
=12.
(1)当f(m)最小时,求此时对应的“加成数”的值;
(2)若f(m)是24的倍数,则称f(m)是“节气数”,猜想这样的“节气数”有多少个,并求出所有的“节气数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
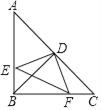
【题目】如图所示,在Rt△ABC中,∠ABC=90°,AB=BC,点D是AC的中点,直角∠EDF的两边分别交AB、BC于点E、F,给出以下结论:①AE=BF;②S四边形BEDF=![]() S△ABC;③△DEF是等腰直角三角形;④当∠EDF在△ABC内绕顶点D旋转时D旋转时(点E不与点A、B重合),∠BFE=∠CDF,上述结论始终成立的有( )个.
S△ABC;③△DEF是等腰直角三角形;④当∠EDF在△ABC内绕顶点D旋转时D旋转时(点E不与点A、B重合),∠BFE=∠CDF,上述结论始终成立的有( )个.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;
②4a﹣2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2 .
上述4个判断中,正确的是( )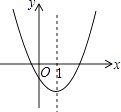
A.①②
B.①④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,∠A′B′C′可以由△ABC绕点C顺时针旋转得到,其中点A′与点A是对应点,点B′与点B是对应点,连接AB′,且A、B′、A′在同一条直线上,则AA′的长为( ) 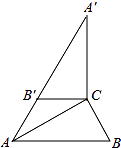
A.4 ![]()
B.6
C.3 ![]()
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为__.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com