
【题目】若一个三位数,其个位数加上十位数等于百位数,可表示为t=100(x+y)+10y+x,则称实数t为“加成数”,将t的百位作为个位,个位作为十位,十位作为百位,组成一个新的三位数h.规定q=t﹣h,f(m)=![]() ,例如:321是一个“加成数”,将其百位作为个位,个位作为十位,十位作为百位,得到的数h=213,∴q=321﹣213=108,f(m)=
,例如:321是一个“加成数”,将其百位作为个位,个位作为十位,十位作为百位,得到的数h=213,∴q=321﹣213=108,f(m)=![]() =12.
=12.
(1)当f(m)最小时,求此时对应的“加成数”的值;
(2)若f(m)是24的倍数,则称f(m)是“节气数”,猜想这样的“节气数”有多少个,并求出所有的“节气数”.
【答案】(1)当x=0,y=1时,q小=9,此时对应的“加成数”是110;(2)这样的“节气数”有4个,分别为24,72.
【解析】
(1)根据新定义,由求f(m)最小值,可知就是求q的最小值,根据定义表示q=t﹣h=100(x+y)+10y+x﹣(101y+11x)=9y+90x,可得结论;
(2)根据f(m)是24的倍数,f(m)=24n(n为正整数),得q=216n,由(1)中q=9y+90x,列方程,解方程可得结论.
(1)∵f(m)=![]() ,
,
∴当f(m)最小时,q最小,
∵t=100(x+y)+10y+x,h=100y+10x+x+y=101y+11x,
∴q=t﹣h=100(x+y)+10y+x﹣(101y+11x)=9y+90x,且1≤y≤9,0≤x≤9,x、y为正整数,
当x=0,y=1时,q小=9,此时对应的“加成数”是110;
(2)∵f(m)是24的倍数,
设f(m)=24n(n为正整数),
则24n=![]() ,q=216n,
,q=216n,
由(1)知:q=9y+90x=9(y+10x),
∴216n=9(y+10x),
24n=y+10x,
①当n=1时,即y+10x=24,解得:x=2,y=4,则这样的“节气数”是24;
②当n=2时,即y+10x=48,解得:x=4,y=8,则这样的“节气数”是48;此时百位上的数为12,舍去.
③当n=3时,即y+10x=72,解得:x=7,y=2,则这样的“节气数”是72;
①当n=4时,即y+10x=96,解得:x=9,y=6,则这样的“节气数”是96;此时百位上的数为15,舍去.
①当n=5时,即y+10x=120,没有符合条件的整数解,
综上,这样的“节气数”有4个,分别为24, 72.


科目:初中数学 来源: 题型:
【题目】关于概率,下列说法正确的是( )
A.莒县“明天降雨的概率是75%”表明明天莒县会有75%的时间会下雨
B.随机抛掷一枚质地均匀的硬币,落地后一定反面向上
C.在一次抽奖活动中,中奖的概率是1%,则抽奖100次就一定会中奖
D.同时抛掷两枚质地均匀硬币,“一枚硬币正面向上,一枚硬币反面向上”的概率是 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
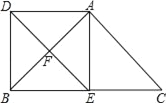
【题目】如图,E、F分别为△ABC的边BC、CA的中点,延长EF到D,使得DF=EF,连接DA、DB、AE.
(1)求证:四边形ACED是平行四边形;
(2)若AB=AC,试说明四边形AEBD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:
①2a+b=0;②4a﹣2b+c<0;③ac>0;④当y<0时,x<﹣1或x>2.
其中正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上. 
(1)连接DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断命题“在旋转的过程中,线段DF与BF的长始终相等”是否正确?答: .
(2)若将正方形AEFG绕点A按顺时针方向旋转,连接DG,在旋转过程中,你能否找到一条线段的长与线段DG的长始终相等?并以图为例说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A、B、C、D四个点,分别对应的数为a,b,c,d,且满足a,b是方程|x+7|=1的两个解(a<b),且(c﹣12)2与|d﹣16|互为相反数.
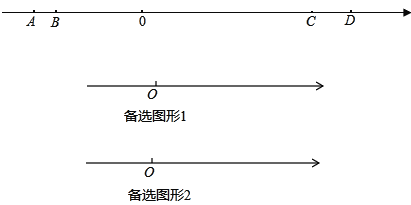
(1)填空:a= 、b= 、c= 、d= ;
(2)若线段AB以3个单位/秒的速度向右匀速运动,同时线段CD以1单位长度/秒向左匀速运动,并设运动时间为t秒,A、B两点都运动在CD上(不与C,D两个端点重合),若BD=2AC,求t得值;
(3)在(2)的条件下,线段AB,线段CD继续运动,当点B运动到点D的右侧时,问是否存在时间t,使BC=3AD?若存在,求t得值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣1,0)及点B. 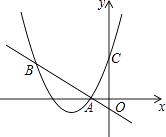
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com