
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:
①2a+b=0;②4a﹣2b+c<0;③ac>0;④当y<0时,x<﹣1或x>2.
其中正确的个数是( )
A.1
B.2
C.3
D.4
【答案】B
【解析】解:∵对称轴为x=1,
∴x=﹣ ![]() =1,
=1,
∴﹣b=2a,
∴①2a+b=0,故此选项正确;
∵点B坐标为(﹣1,0),
∴当x=﹣2时,4a﹣2b+c<0,故此选项正确;
∵图象开口向下,∴a<0,
∵图象与y轴交于正半轴上,
∴c>0,
∴ac<0,故ac>0错误;
∵对称轴为x=1,点B坐标为(﹣1,0),
∴A点坐标为:(3,0),
∴当y<0时,x<﹣1或x>3,
故④错误;
故选:B.
【考点精析】本题主要考查了二次函数图象以及系数a、b、c的关系的相关知识点,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图△ABC是正三角形,曲线CDEF叫做“正三角形的渐开线”,其中 ![]() 、
、 ![]() 、
、 ![]() 圆心依次按A、B、C…循环,它们依次相连接.若AB=1,则曲线CDEF长是(结果保留π).
圆心依次按A、B、C…循环,它们依次相连接.若AB=1,则曲线CDEF长是(结果保留π). 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)△ABC的面积为__________;
(2)在图中作出△ABC关于直线MN的对称图形△A′B′C′.
(3)利用网格纸,在MN上找一点P,使得PB+PC的距离最短.( 保留痕迹)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+m.
(1)如果二次函数的图象与x轴有两个交点,求m的取值范围;
(2)如图,二次函数的图象过点A(3,0),与y轴交于点B,直线AB与这个二次函数图象的对称轴交于点P,求点P的坐标. 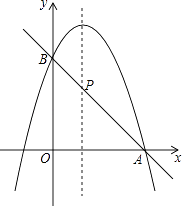
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE交BD于G,交BC于H,下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=![]() (∠BAC﹣∠C);④∠BGH=∠ABE+∠C.
(∠BAC﹣∠C);④∠BGH=∠ABE+∠C.
其中正确的是( )

A. ①②③ B. ①③④ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三位数,其个位数加上十位数等于百位数,可表示为t=100(x+y)+10y+x,则称实数t为“加成数”,将t的百位作为个位,个位作为十位,十位作为百位,组成一个新的三位数h.规定q=t﹣h,f(m)=![]() ,例如:321是一个“加成数”,将其百位作为个位,个位作为十位,十位作为百位,得到的数h=213,∴q=321﹣213=108,f(m)=
,例如:321是一个“加成数”,将其百位作为个位,个位作为十位,十位作为百位,得到的数h=213,∴q=321﹣213=108,f(m)=![]() =12.
=12.
(1)当f(m)最小时,求此时对应的“加成数”的值;
(2)若f(m)是24的倍数,则称f(m)是“节气数”,猜想这样的“节气数”有多少个,并求出所有的“节气数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;
②4a﹣2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2 .
上述4个判断中,正确的是( )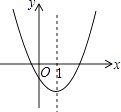
A.①②
B.①④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折得到△FMN,若MF∥AD,FN∥DC,则∠D的度数为( )
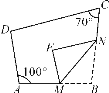
A. 115° B. 105° C. 95° D. 85°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com