
【题目】如图△ABC是正三角形,曲线CDEF叫做“正三角形的渐开线”,其中 ![]() 、
、 ![]() 、
、 ![]() 圆心依次按A、B、C…循环,它们依次相连接.若AB=1,则曲线CDEF长是(结果保留π).
圆心依次按A、B、C…循环,它们依次相连接.若AB=1,则曲线CDEF长是(结果保留π). 
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,AB∥DC,连接BD,BE平分∠ABD,BE⊥AD,∠EBC和∠DCB的角平分线相交于点F,若∠ADC=110°,则∠F的度数为( )
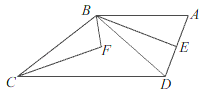
A. 115° B. 110° C. 105° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+2x+a﹣2=0.
(1)若该方程有两个不相等的实数根,求实数a的取值范围;
(2)当该方程的一个根为1时,求a的值及方程的另一根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于概率,下列说法正确的是( )
A.莒县“明天降雨的概率是75%”表明明天莒县会有75%的时间会下雨
B.随机抛掷一枚质地均匀的硬币,落地后一定反面向上
C.在一次抽奖活动中,中奖的概率是1%,则抽奖100次就一定会中奖
D.同时抛掷两枚质地均匀硬币,“一枚硬币正面向上,一枚硬币反面向上”的概率是 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
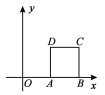
【题目】如图,在平面直角坐标系中,已知A(1,0),B(2,0),四边形ABCD是正方形.
(1)写出C,D两点坐标;
(2)将正方形ABCD绕O点逆时针旋转90°后所得四边形的四个顶点的坐标分别是多少?
(3)若将(2)所得的四边形再绕O点逆时针旋转90°后,所得四边形的四个顶点坐标又分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某闭合电路中,其两端电压恒定,电流I(A)与电阻R(Ω)图象如图所示,回答问题: 
(1)写出电流I与电阻R之间的函数解析式.
(2)如果一个用电器的电阻为5Ω,其允许通过的最大电流是1A,那么这个用电器接在这个闭合电路中,会不会烧毁?说明理由.
(3)若允许的电流不超过4A时,那么电阻R的取值应该控制在什么范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于概率,下列说法正确的是( )
A.莒县“明天降雨的概率是75%”表明明天莒县会有75%的时间会下雨
B.随机抛掷一枚质地均匀的硬币,落地后一定反面向上
C.在一次抽奖活动中,中奖的概率是1%,则抽奖100次就一定会中奖
D.同时抛掷两枚质地均匀硬币,“一枚硬币正面向上,一枚硬币反面向上”的概率是 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y= ![]() 在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )
在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( ) 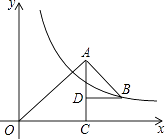
A.36
B.12
C.6
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:
①2a+b=0;②4a﹣2b+c<0;③ac>0;④当y<0时,x<﹣1或x>2.
其中正确的个数是( )
A.1
B.2
C.3
D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com