
����Ŀ����a��b��������������ʵ�������ǹ涨�����㲻��ʽa��x��b��ʵ��x������ȡֵ��ȫ����������䣬��ʾΪ[a��b]������һ����������������Ա���x�뺯��ֵy���㣺��m��x��nʱ����m��y��n�����Ǿͳƴ˺����DZ�����[m��n]�ϵġ��պ��������纯��y=��x+4����x=1ʱ��y=3����x=3ʱ��y=1������1��x��3ʱ������1��y��3������˵����y=��x+4�DZ�����[1��3]�ϵġ��պ�������ͬ������y=xҲ�DZ�����[1��3]�ϵġ��պ�������
��1������������y=![]() �DZ�����[1��2018]�ϵġ��պ����������жϲ�˵�����ɣ�
�DZ�����[1��2018]�ϵġ��պ����������жϲ�˵�����ɣ�
��2�������֪���κ���y=x2��4x+k�DZ�����[2��t]�ϵġ��պ���������k��t��ֵ��
��3�������2�������Ķ��κ�����ͼ��y����C�㣬AΪ�˶��κ���ͼ��Ķ��㣬BΪֱ��x=1�ϵ�һ�㣬����ABCΪֱ��������ʱ��д����B�����꣮
���𰸡���1������������y=![]() �DZ�����[1��2018]�ϵġ��պ�������2��t=3��3������ABCΪֱ��������ʱ����B�����꣨1��4+
�DZ�����[1��2018]�ϵġ��պ�������2��t=3��3������ABCΪֱ��������ʱ����B�����꣨1��4+![]() ������1��4��
������1��4��![]() ������1��
������1��![]() ������1��
������1��![]() ��
��
�������������� ��1����k��0��֪����������y=![]() �ڱ�����[1��2016]��y��x���������С��Ȼ��x=1��x=2018����뷴��������ʽ�Ľ���ʽ���Ӷ������y�ķ�Χ�����ǿ������жϣ�
�ڱ�����[1��2016]��y��x���������С��Ȼ��x=1��x=2018����뷴��������ʽ�Ľ���ʽ���Ӷ������y�ķ�Χ�����ǿ������жϣ�
��2������ö��κ����ĶԳ���Ϊx=1��a=1��0�����ݶ��κ��������ʿ�֪y=x2-4x+k�ڱ�����[2��t]��y��x�����������Ȼ��x=2��y=k-4��x=t��y=t2-4t+k�ֱ������κ����Ľ���ʽ���Ӷ������k��ֵ��
��3�����ݹ��ɶ������涨�����ɵ÷��̣����ݽⷽ�̣��ɵô𰸣�
��⣺
��1����k=2018��
����1��x��2018ʱ��y��x���������С��
����x=1ʱ��y=2018��x=2018ʱ��y=1��
��1��y��2108��
������������y=![]() �DZ�����[1��2018]�ϵġ��պ�������
�DZ�����[1��2018]�ϵġ��պ�������
��2����x=��![]() =2��a=1��0��
=2��a=1��0��
�����κ���y=x2��4x+k�ڱ�����[2��t]��y��x�����������
�����κ���y=x2��2x��k�DZ�����[2��t]�ϵġ��պ�������
����x=2ʱ��y=k��4��x=tʱ��y=t2��4t+k��
![]() ��
��
���k=6��t=3��t=��2��
��Ϊt��2��
��t=2��ȥ��
��t=3��
��3���ɶ��κ�����ͼ��y����C�㣬AΪ�˶��κ���ͼ��Ķ��㣬��
A��2��2����C��0��6����B��1��t����
�ɹ��ɶ�������AC2=22+��2��6��2��AB2=��2��1��2+��2��t��2��BC2=12+��t��6��2��
������ABC=90��ʱ��AB2+BC2=AC2����
��2��1��2+��2��t��2+��t��6��2+1=22+��2��6��2��
����t2��8t+11=0�����t=4+![]() ��t=4��
��t=4��![]() ��
��
B��1��4+![]() ������1��4��
������1��4��![]() ����
����
������BAC=90���ǣ�AB2+AC2=BC2��
����2��1��2+��2��t��2+22+��2��6��2=12+��t��6��2��
����8t=12��
���t=![]() ��
��
B��1��![]() ����
����
������ACB=90��ʱ��AC2+CB2=AB2��
��22+��2��6��2+12+��t��6��2=��2��1��2+��2��t��2��
����2t=13��
���t=![]() ��
��
B��1��![]() ����
����
��������������ABCΪֱ��������ʱ����B�����꣨1��4+![]() ������1��4��
������1��4��![]() ������1��
������1��![]() ������1��
������1��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ᳫ���ж��л����䣬Ӫ������У���������ж���Χ���ٽ�У�Ļ����裬��������ѧ���������ж�ϰ�ߣ�ʹ����֮�����У��ij��ѧΪ���˽�ѧ��ÿ����У�����ж�ʱ�䣬�ڱ�У�����ȡ��������ѧ�����е��飬�����ݵ��������������²�������ͳ��ͼ���������ͼ����Ϣ����������⣺
ʱ�䣨Сʱ�� | Ƶ���������� | Ƶ�� |
2��t��3 | 4 | 0.1 |
3��t��4 | 10 | 0.25 |
4��t��5 | a | 0.15 |
5��t��6 | 8 | b |
6��t��7 | 12 | 0.3 |
�ϼ� | 40 | 1 |
��1�����е�a���� ����b���� ����
��2���뽫Ƶ���ֲ�ֱ��ͼ��ȫ��
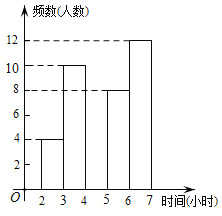
��3������У����1200��ѧ�����Թ���ȫУÿ����У�μӾ����ж�ʱ��������4Сʱ��ѧ��ԼΪ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
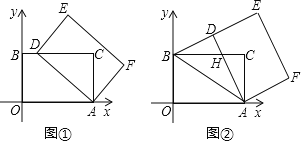
����Ŀ����ƽ��ֱ������ϵ�У��ı���AOBC�Ǿ��Σ���O��0��0������A��5��0������B��0��3�����Ե�AΪ���ģ�˳ʱ����ת����AOBC���õ�����ADEF����O��B��C�Ķ�Ӧ��ֱ�ΪD��E��F��
��1����ͼ�٣�����D����BC����ʱ�����D�����ꣻ
��2����ͼ�ڣ�����D�����߶�BE��ʱ��AD��BC���ڵ�H��
����֤��ADB�ա�AOB��
�����H�����꣮
��3����KΪ����AOBC�Խ��ߵĽ��㣬SΪ��KDE���������S��ȡֵ��Χ��ֱ��д��������ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��Ӧ��ɫ���к�����Խ��Խ������ѡ�����ù���������������֪ij����������˾Ϊ�����ṩ���ֻ�֧���ͻ�Ա��֧������֧����ʽ����ͼ���������ַ�ʽӦ֧�����y(Ԫ)������ʱ��x(ʱ)֮��ĺ�����ϵ������ͼ��ش��������⣺
(1)���ֻ�֧�����y(Ԫ)������ʱ��x(ʱ)�ĺ�����ϵʽ��
(2)����ʦ�������й�������������ݲ�ͬ������ʱ�����ȷ��ѡ������֧����ʽ�ȽϺ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ���ڽ���120�㣬����һ���Խ��߳�Ϊ9�������εı߳�Ϊ____________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪:��ƽ��ֱ������ϵ![]() ��,ֱ��
��,ֱ��![]() �ֱ�
�ֱ�![]() ��
��![]() ���ڵ�A��B����,OA=5,��OAB=60��.
���ڵ�A��B����,OA=5,��OAB=60��.
(1)��ͼ1,��ֱ��AB�Ľ���ʽ��
(2)��ͼ2,��PΪֱ��AB��һ�㣬����OP,��D��OA�ӳ����ϣ��ֱ����P��D��OA��OP��ƽ����,��ƽ���߽��ڵ�C������AC,��AD=m,��ABC�����ΪS,��S��m�ĺ�����ϵʽ;
(3)��ͼ3,��(2)��������,��PA��ȡ��E ,ʹPE=AD, ����EC,DE,����ECD=60��,�ı���ADCE���ܳ�����22����S��ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
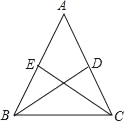
����Ŀ����ͼ������������ABC�У�BD��CE�ֱ��������ϵ����ߣ�
��1����֤��BD=CE��
��2����BD��CE�ཻ�ڵ�O����M��N�ֱ�Ϊ�߶�BO��CO���е㣬����ABC�����ĵ�����A�ľ�����ױ߳����ʱ���ж��ı���DEMN����״������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ1��һ�������Σ��ֱ�����������������ߵ��е�õ�ͼ2���ٷֱ�����ͼ2�м�С�����ε��е㣬�õ�ͼ3�������������к����������������룩



�����淽��������ȥ����20��ͼ��_____�������Σ���n��ͼ����_____�������Σ�����n�Ĵ���ʽ��ʾ���ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
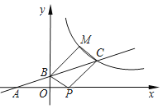
����Ŀ����ͼ��ʾ��ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ���뷴������
���뷴������![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() ����
����![]() ��
��
��1�����![]() ������ͷ���������
������ͷ���������![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����![]() ��
��![]() ���ϣ�����������
���ϣ�����������![]() ͼ���ϴ��ڵ�
ͼ���ϴ��ڵ�![]() ��ʹ���ı���
��ʹ���ı���![]() Ϊƽ���ı��Σ�����M�����꣮
Ϊƽ���ı��Σ�����M�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com