
【题目】菱形有一个内角是120°,其中一条对角线长为9,则菱形的边长为____________.
科目:初中数学 来源: 题型:
【题目】阅读:能够成为直角三角形三条边长的三个正整数a,b,c,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组公式为: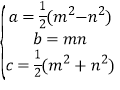 其中m>n>0,m,n是互质的奇数.
其中m>n>0,m,n是互质的奇数.
应用:当n=1时,求有一边长为5的直角三角形的另外两条边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+4的图象与反比例函数y=![]() (k≠0)的图象交于A(1,a)、B(b,1)两点.
(k≠0)的图象交于A(1,a)、B(b,1)两点.
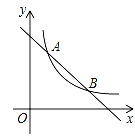
(1)求反比例函数的表达式;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标;
(3)在(2)的条件下,求△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果点A(0,2)和点B(4,2)都在二次函数y=x2+bx+c的图象上,那么此抛物线在直线_____的部分是上升的.(填具体某直线的某侧)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E是BC边上的点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)如图①,当点E是BC边上任一点(不与点B、C重合)时,求证:AE=EF.
(2)如图②当点E是BC边的延长线上一点时,(1)中的结论还成立吗? (填成立或者不成立).
(3)当点E是BC边上任一点(不与点B、C重合)时,若已知AE=EF,那么∠AEF的度数是否发生变化?证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.如函数y=﹣x+4,当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,恒有1≤y≤3,所以说函数y=﹣x+4是闭区间[1,3]上的“闭函数”,同理函数y=x也是闭区间[1,3]上的“闭函数”.
(1)反比例函数y=![]() 是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
(2)如果已知二次函数y=x2﹣4x+k是闭区间[2,t]上的“闭函数”,求k和t的值;
(3)如果(2)所述的二次函数的图象交y轴于C点,A为此二次函数图象的顶点,B为直线x=1上的一点,当△ABC为直角三角形时,写出点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AD∥BC,AD=CD,BC=AC,∠BAD=108°,则∠D=( )
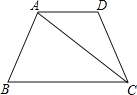
A. 144°B. 110°C. 100°D. 108°
查看答案和解析>>
科目:初中数学 来源: 题型:
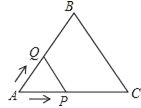
【题目】如图,等边△ABC的边长为2cm,点P从点A出发,以1cm/s的速度沿AC向点C运动,到达点C停止;同时点Q从点A出发,以2cm/s的速度沿AB﹣BC向点C运动,到达点C停止,设△APQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
A. 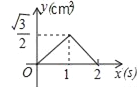 B.
B. 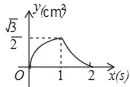
C. 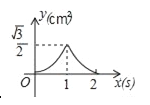 D.
D. 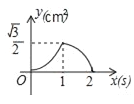
查看答案和解析>>
科目:初中数学 来源: 题型:
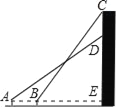
【题目】如图所示,小王在校园上的A处正面观测一座教学楼墙上的大型标牌,测得标牌下端D处的仰角为30°,然后他正对大楼方向前进5m到达B处,又测得该标牌上端C处的仰角为45°.若该楼高为16.65m,小王的眼睛离地面1.65m,大型标牌的上端与楼房的顶端平齐.求此标牌上端与下端之间的距离(![]() ≈1.732,结果精确到0.1m).
≈1.732,结果精确到0.1m).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com