
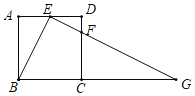
【题目】如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且∠BEF=90°,延长EF交BC的延长线于点G.
(1)求证:△ABE∽△EGB.
(2)若AB=4,求CG的长.
【答案】(1)证明见解析;(2)CG=6.
【解析】
(1)由正方形的性质与已知得出∠A=∠BEG,证出∠ABE=∠G,即可得出结论;
(2)由AB=AD=4,E为AD的中点,得出AE=DE=2,由勾股定理得出BE=![]() ,由△ABE∽△EGB,得出
,由△ABE∽△EGB,得出![]() ,求得BG=10,即可得出结果.
,求得BG=10,即可得出结果.
(1)证明:∵四边形ABCD为正方形,且∠BEG=90°,
∴∠A=∠BEG,
∵∠ABE+∠EBG=90°,∠G+∠EBG=90°,
∴∠ABE=∠G,
∴△ABE∽△EGB;
(2)∵AB=AD=4,E为AD的中点,
∴AE=DE=2,
在Rt△ABE中,BE=![]() ,
,
由(1)知,△ABE∽△EGB,
∴![]() ,即:
,即:![]() ,
,
∴BG=10,
∴CG=BG﹣BC=10﹣4=6.


科目:初中数学 来源: 题型:
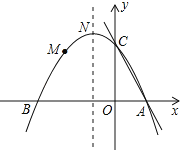
【题目】如图,抛物线y=ax2+bx+c(a≠0)的图象过点M(﹣2,![]() ),顶点坐标为N(﹣1,
),顶点坐标为N(﹣1,![]() ),且与x轴交于A、B两点,与y轴交于C点.
),且与x轴交于A、B两点,与y轴交于C点.
(1)求抛物线的解析式;
(2)点P为直线y=﹣1上的动点,Q是抛物线线上的动点,若以A,C,P,Q为顶点的四边形是平行四边形,求点P的坐标;
(3)在直线AC上是否存在一点Q,使△QBM的周长最小?若存在,求出Q点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
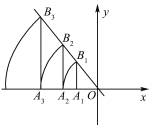
【题目】如图,直线l:y=-![]() x,点A1的坐标为(-3,0). 过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…按此做法进行下去,点A2 017的坐标为 ( )
x,点A1的坐标为(-3,0). 过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…按此做法进行下去,点A2 017的坐标为 ( )
A.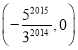 B.
B.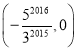 C.
C.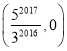 D.
D.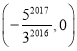
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1 ,它与x轴交于两点O,A;将C1绕点A旋转180°得到C2 , 交x轴于A1;将C2绕点A1旋转180°得到C3 , 交x轴于点A2 . .....如此进行下去,直至得到C2018 , 若点P(4035,m)在第2018段抛物线上,则m的值为________.
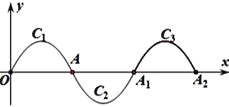
查看答案和解析>>
科目:初中数学 来源: 题型:
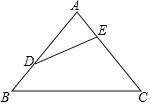
【题目】如图,△ABC中,AB=AC,∠A=80°,点D,E分别在边AB,AC上,且DA=DE=CE.
(1)求作点F,使得四边形BDEF为平行四边形;(要求:尺规作图,保留痕迹,不写作法)
(2)连接CF,写出图中经过旋转可完全重合的两个三角形,并指出旋转中心和旋转角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象与x轴交于A(﹣3,0)和B(1,0)两点,交y轴于点C(0,3),点C、D是二次函数图象上的一对对称点,一次函数的图象过点B、D.
(1)请直接写出D点的坐标.
(2)求二次函数的解析式.
(3)根据图象直接写出使一次函数值大于二次函数值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:有一内角为直角的三角形叫做直角三角形.类似地我们定义:有一内角为45°的三角形叫做半直角三角形.如图,在平面直角坐标系中,O为原点,A(4,0),B(-4,0),D是y轴上的一个动点,∠ADC=90°(A、D、C按顺时针方向排列), BC与经过A、B、D三点的⊙M交于点E,DE平分∠ADC,连结AE,BD.显然ΔDCE、ΔDEF、ΔDAE是半直角三角形.
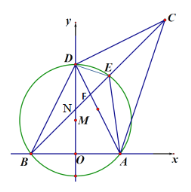
(1)求证:ΔABC是半直角三角形;
(2)求证:∠DEC=∠DEA;
(3)若点D的坐标为(0,8),求AE的长;
(4)BC交y轴于点N,问![]() 的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经过市场调查,整理出某种商品在第x(x≤90)天的售价与销量的相关信息如右表.已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元件) | x+40 | 90 |
每天销量(件) | 200-2x | |
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD,我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
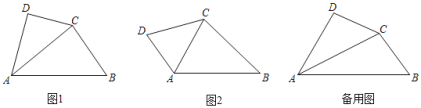
(1)如图2,四边形ABCD为“可分四边形”,∠DAB为“可分角”,求证:△DAC∽△CAB.
(2)如图2,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则∠DAB= °
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,BC=2,∠D=90°,求AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com