
【题目】我们知道:有一内角为直角的三角形叫做直角三角形.类似地我们定义:有一内角为45°的三角形叫做半直角三角形.如图,在平面直角坐标系中,O为原点,A(4,0),B(-4,0),D是y轴上的一个动点,∠ADC=90°(A、D、C按顺时针方向排列), BC与经过A、B、D三点的⊙M交于点E,DE平分∠ADC,连结AE,BD.显然ΔDCE、ΔDEF、ΔDAE是半直角三角形.
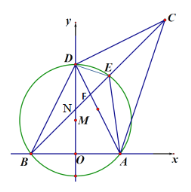
(1)求证:ΔABC是半直角三角形;
(2)求证:∠DEC=∠DEA;
(3)若点D的坐标为(0,8),求AE的长;
(4)BC交y轴于点N,问![]() 的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
的值是否发生变化?若不发生变化,请求出其值;若发生变化,请说明理由.
【答案】(1)见解析;(2)见解析;(3)![]() ;(4)
;(4)![]() 不变,为
不变,为 ![]() .
.
【解析】
(1)先求得∠ADE=45°,由同弧所对的圆周角可知:∠ABE=∠ADE=45°,根据定义得:△ABC是半直角三角形;
(2)根据垂直平分线的性质得:AD=BD,由等角对等边得:∠DAB=∠DBA,由D、B、A、E四点共圆,
则∠DBA+∠DEA=180°,可得结论;
(3)设⊙M的半径为r,根据勾股定理列方程为:(8-r)2+42=r2,可得⊙M的半径为5,由同弧所对的圆心角和圆周角的关系可得∠EMA=2∠ABE=90°,根据勾股定理可得结论;
(4)过点C作CH⊥DO于H,过点C作CQ⊥BA于Q,通过证明Rt△HDC≌Rt△ADO,推出HC=OD,DH=OA,推出CQ= BQ,得出∠CBQ=45°,推出△HCN为等腰直角三角形即可.
解:(1)∵∠ADC=90°,DE平分∠ADC,
∴∠ABE=∠ADE=45
∴ΔABC是半直角三角形
(2))∵OM⊥AB,OA=OB,
∴AD=BD,
∴∠DAB=∠DBA,
∵∠DEB=∠DAB,
∴∠DBA=∠DEB,
∵D、B、A、E四点共圆,
∴∠DBA+∠DEA=180°,
∵∠DEB+∠DEC=180°,
∴∠DEA=∠DEC;
(3))①如图,连接AM,ME,设⊙M的半径为r,
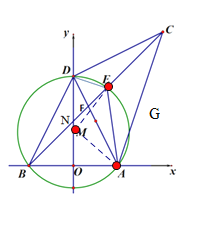
∵点D的坐标为(0,8)∴OM=8-r
由![]() 得
得![]() 解得r=5 ∴⊙M 的半径为5
解得r=5 ∴⊙M 的半径为5
∵∠ABE=45°
∴∠EMA=2∠ABE=90°,
∴EA2=MA2+ME2=52+52=50
∴![]()
(4)![]() 不变,为
不变,为 ![]()
过点C作CH⊥DO于H,过点C作CQ⊥BA于Q,
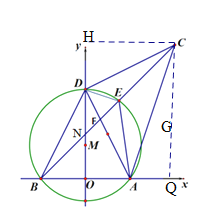
∵∠CDH+∠ODA=90°,∠CDH+∠CDH=90°,
∴∠ODA=∠CDA,
在△HDC和△ADO中,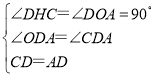
∴Rt△HDC≌Rt△ADO(AAS),
∴HC=OD,DH=OA,
又∵BO=AO,
∴HO=DH+DO=OB+CH,
而
∴CQ=OB+OQ=BQ,
∴∠CBQ=45°,
又∵CH∥BA,
∴∠HCN=45°,
∴△HCN为等腰直角三角形,
∴![]()
∴![]() =
=![]()


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.
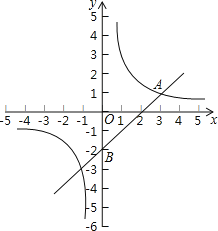
查看答案和解析>>
科目:初中数学 来源: 题型:
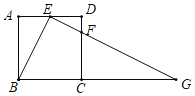
【题目】如图,△ABC中,∠B=10°,∠ACB=20°,AB=4cm,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD的中点.

(1)指出旋转中心,并求出旋转的度数;
(2)求出∠BAE的度数和AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
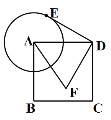
【题目】如图,在正方形ABCD中,E为边AD的中点,点F在边CD上,且∠BEF=90°,延长EF交BC的延长线于点G.
(1)求证:△ABE∽△EGB.
(2)若AB=4,求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为4,以点A为圆心,2为半径作圆,E是⊙A上的任意一点,将点E绕点D按逆时针方向转转90°得到点F,则线段AF的长的最小值____.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
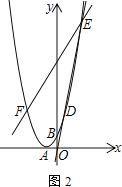
【题目】已知抛物线顶点![]() 在
在![]() 轴负半轴上,与
轴负半轴上,与![]() 轴交于点
轴交于点![]() ,
,![]() ,
,![]() 为等腰直角三角形.
为等腰直角三角形.
(1)求抛物线的解析式
(2)若点![]() 在抛物线上,若
在抛物线上,若![]() 为直角三角形,求点
为直角三角形,求点![]() 的坐标
的坐标
(3)已知直线![]() 过点
过点![]() ,交抛物线于点
,交抛物线于点![]() 、
、![]() ,过
,过![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,求证:直线
,求证:直线![]() 经过一个定点,并求定点的坐标.
经过一个定点,并求定点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
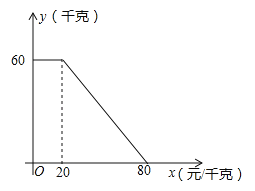
【题目】某商店以20元/千克的单价新进一批商品,经调查发现,在一段时间内,销售量y(千克)与销售单价x(元/千克)之间为一次函数关系,如图所示.
(1)求y与x的函数表达式;
(2)要使销售利润达到800元,销售单价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,F是AB上一点,H是BC延长线上一点,连接FH,将△FBH沿FH翻折,使点B的对应点E落在AD上,EH与CD交于点G,连接BG交FH于点M,当GB平分∠CGE时,BM=2![]() ,AE=8,则ED=______.
,AE=8,则ED=______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com