
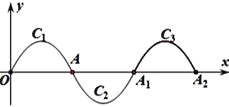
【题目】如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1 ,它与x轴交于两点O,A;将C1绕点A旋转180°得到C2 , 交x轴于A1;将C2绕点A1旋转180°得到C3 , 交x轴于点A2 . .....如此进行下去,直至得到C2018 , 若点P(4035,m)在第2018段抛物线上,则m的值为________.
【答案】-1
【解析】
每次变化时,开口方向变化但形状不变,则 ![]() ,故开口向上时a=1,开口向下时a=-1;与x轴的交点在变化,可发现规律抛物线Cn与x轴交点的规律是(2n-2,0)和(2n,0),由两点式
,故开口向上时a=1,开口向下时a=-1;与x轴的交点在变化,可发现规律抛物线Cn与x轴交点的规律是(2n-2,0)和(2n,0),由两点式![]() 求得解析式,把x=4035代入解析式,即可求得m的值.
求得解析式,把x=4035代入解析式,即可求得m的值.
由抛物线C1:y=-x(x-2),
令y=0,∴-x(x-2)=0,解得 ![]()
∴与x轴的交点为O(0,0),A(2,0).
抛物线C2的开口向上,且与x轴的交点为∴A(2,0)和A1(4,0),
则抛物线C2:y= (x-2)(x-4);
抛物线C3的开口向下,且与x轴的交点为∴A1(4,0)和A2(6,0),
则抛物线C3:y= -(x-4)(x-6);
抛物线C4的开口向上,且与x轴的交点为∴A2(6,0)和A3(8,0),
则抛物线C4:y=(x-6)(x-8);
同理:
抛物线C2018的开口向上,且与x轴的交点为∴A2016(4034,0)和A2017(4036,0),
则抛物线C2018:y=(x-4034)(x-4036);
当x=4035时,y= 1×(-1)-1.
故答案为:-1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,甲、乙两城决定向![]() 、
、![]() 两乡运送肥料以支持农村生产,已知甲、乙两城共有肥料800吨,其中乙城肥料是甲城的2倍少100吨,从甲城往
两乡运送肥料以支持农村生产,已知甲、乙两城共有肥料800吨,其中乙城肥料是甲城的2倍少100吨,从甲城往![]() 、
、![]() 两乡运肥料的费用分别为20元吨和25元吨;从乙城往
两乡运肥料的费用分别为20元吨和25元吨;从乙城往![]() 、
、![]() 两乡运肥料的费用分别为15元吨和26元吨.现
两乡运肥料的费用分别为15元吨和26元吨.现![]() 乡需要肥料440吨,
乡需要肥料440吨,![]() 乡需要肥料360吨.
乡需要肥料360吨.
(1)甲城和乙城各有多少吨肥料?
(2)设从甲城运往![]() 乡肥料
乡肥料![]() 吨,总运费为
吨,总运费为![]() 元,求出最少总运费.
元,求出最少总运费.
(3)由于更换车型,使甲城运往![]() 乡的运费每吨减少
乡的运费每吨减少![]() 元,这时从甲城运往
元,这时从甲城运往![]() 乡肥料多少吨才能使总运费最少,最少是多少?
乡肥料多少吨才能使总运费最少,最少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
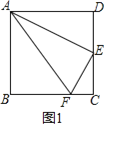
【题目】如图1,在正方形![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 边上一点,且
边上一点,且![]() .
.
(1)求证:![]() ;
;
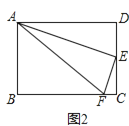
(2)将“正方形”改成“矩形”,其他条件均不变,如图2,你认为仍然有“![]() ”吗?若你同意,请以图2为例加以证明;若你不同意,请说明理由.
”吗?若你同意,请以图2为例加以证明;若你不同意,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰三角形△ABC中,O为底边BC的中点,以O为圆心作半圆与AB,AC相切,切点分别为D,E.过半圆上一点F作半圆的切线,分别交AB,AC于M,N.那么![]() 的值等于( )
的值等于( )
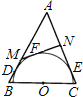
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
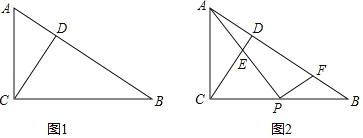
【题目】在△ABC中,∠ACB=90°,CD为高,BC=nAC
(1)如图1,当n=![]() 时,则
时,则![]() 的值为 ;(直接写出结果)
的值为 ;(直接写出结果)
(2)如图2,点P是BC的中点,过点P作PF⊥AP交AB于F,求![]() 的值;(用含n的代数式表示)
的值;(用含n的代数式表示)
(3)在(2)的条件下,若PF=BF,则n= .(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鄂州市化工材料经销公司购进一种化工原料若干千克,价格为每千 克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时 ,y=80;x=50时,y=100.在销售过程中,每天还要支付其他费用450元.
(1)(3分)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)(3分)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式.
(3)(4分)当销售单价为多少元时,该公司日获利最大?最大获利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx(a>0)过点E(8,0),矩形ABCD的边AB在线段OE上(点A在点B的左侧),点C、D在抛物线上,∠BAD的平分线AM交BC于点M,点N是CD的中点,已知OA=2,且OA:AD=1:3.
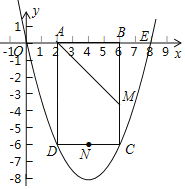
(1)求抛物线的解析式;
(2)F、G分别为x轴,y轴上的动点,顺次连接M、N、G、F构成四边形MNGF,求四边形MNGF周长的最小值;
(3)在x轴下方且在抛物线上是否存在点P,使△ODP中OD边上的高为![]() ?若存在,求出点P的坐标;若不存在,请说明理由;
?若存在,求出点P的坐标;若不存在,请说明理由;
(4)矩形ABCD不动,将抛物线向右平移,当平移后的抛物线与矩形的边有两个交点K、L,且直线KL平分矩形的面积时,求抛物线平移的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
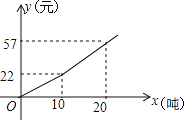
【题目】为鼓励市民节约用水,某市自来水公司按分段收费标准收费,右图反映的是每月收水费y(元)与用水量x(吨)之间的函数关系
(1)小红家五月份用水8吨,应交水费_____元;
(2)按上述分段收费标准,小红家三、四月份分别交水费36元和19.8元,问四月份比三月份节约用水多少吨?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com