
【题目】为了落实党的“精准扶贫”政策,甲、乙两城决定向![]() 、
、![]() 两乡运送肥料以支持农村生产,已知甲、乙两城共有肥料800吨,其中乙城肥料是甲城的2倍少100吨,从甲城往
两乡运送肥料以支持农村生产,已知甲、乙两城共有肥料800吨,其中乙城肥料是甲城的2倍少100吨,从甲城往![]() 、
、![]() 两乡运肥料的费用分别为20元吨和25元吨;从乙城往
两乡运肥料的费用分别为20元吨和25元吨;从乙城往![]() 、
、![]() 两乡运肥料的费用分别为15元吨和26元吨.现
两乡运肥料的费用分别为15元吨和26元吨.现![]() 乡需要肥料440吨,
乡需要肥料440吨,![]() 乡需要肥料360吨.
乡需要肥料360吨.
(1)甲城和乙城各有多少吨肥料?
(2)设从甲城运往![]() 乡肥料
乡肥料![]() 吨,总运费为
吨,总运费为![]() 元,求出最少总运费.
元,求出最少总运费.
(3)由于更换车型,使甲城运往![]() 乡的运费每吨减少
乡的运费每吨减少![]() 元,这时从甲城运往
元,这时从甲城运往![]() 乡肥料多少吨才能使总运费最少,最少是多少?
乡肥料多少吨才能使总运费最少,最少是多少?
【答案】(1)甲城有300吨肥料,乙城有500吨肥料;(2)![]() ;(3)当
;(3)当![]() 时,从甲城运往
时,从甲城运往![]() 乡肥料0吨才能使总运费最少,最少是15660元,当
乡肥料0吨才能使总运费最少,最少是15660元,当![]() 时,从甲城运往
时,从甲城运往![]() 乡肥料300吨才能使总运费最少,最少是
乡肥料300吨才能使总运费最少,最少是![]() 元
元
【解析】
(1)设甲城有![]() 吨肥料,乙城有
吨肥料,乙城有![]() 吨肥料,根据甲、乙两城共有肥料800吨,其中乙城肥料是甲城的2倍少100吨,列方程组得解答即可;
吨肥料,根据甲、乙两城共有肥料800吨,其中乙城肥料是甲城的2倍少100吨,列方程组得解答即可;
(2)设从甲城运往![]() 乡肥料
乡肥料![]() 吨,总运费为
吨,总运费为![]() 元,用含x的代数式分别表示出从甲城运往A乡的肥料吨数,从乙城运往B乡肥料吨数,然后根据:运费=运输吨数x运输费用,得一次函数解析式,利用一次函数的性质解答即可;
元,用含x的代数式分别表示出从甲城运往A乡的肥料吨数,从乙城运往B乡肥料吨数,然后根据:运费=运输吨数x运输费用,得一次函数解析式,利用一次函数的性质解答即可;
(3)列出当甲城运往A乡的运费每吨减少![]() 元时的一次函数解析式,利用一次函数的性质分类讨论即可解答.
元时的一次函数解析式,利用一次函数的性质分类讨论即可解答.
(1)解:设甲城有![]() 吨肥料,乙城有
吨肥料,乙城有![]() 吨肥料.
吨肥料.
![]() 解得
解得![]()
答:甲城有300吨肥料,乙城有500吨肥料
(2)![]()
∵![]()
∴![]() 随
随![]() 的增大而增大,
的增大而增大,
∴当![]() 时,
时,![]()
(3)![]()
当![]() 时,
时,![]() ,
,![]() 随
随![]() 的增大而增大,当
的增大而增大,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 随
随![]() 的增大而减小,当
的增大而减小,当![]() 时,
时,![]() ,
,
答:当![]() 时,从甲城运往
时,从甲城运往![]() 乡肥料0吨才能使总运费最少,最少是15660元,
乡肥料0吨才能使总运费最少,最少是15660元,
当![]() 时,从甲城运往
时,从甲城运往![]() 乡肥料300吨才能使总运费最少,最少是
乡肥料300吨才能使总运费最少,最少是![]() 元
元


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
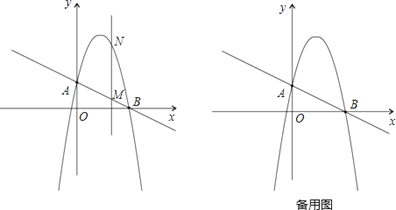
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你用学习“一次函数”时积累的经验和方法研究函数![]() 的图象和性质,并解决问题.
的图象和性质,并解决问题.
![]() 完成下列步骤,画出函数
完成下列步骤,画出函数![]() 的图象;
的图象;
![]() 列表、填空;
列表、填空;
x |
|
|
|
| 0 | 1 | 2 | 3 |
|
y |
| 3 | ______ | 1 | ______ | 1 | 2 | 3 |
|
![]() 描点:
描点:
![]() 连线
连线
![]() 观察图象,当x______时,y随x的增大而增大;
观察图象,当x______时,y随x的增大而增大;
![]() 结合图象,不等式
结合图象,不等式![]() 的解集为______.
的解集为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,量角器的直径与直角三角板ABC的斜边AB重合,其中量角器零刻度线的端点N与点A重合,射线CP从CA处出发沿顺时针方向以每秒4度的速度旋转,CP与量角器的半圆弧交于点E,第18秒时,点E在量角器上对应的读数是__________度.
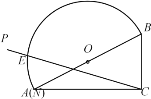
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于A(﹣2,0),点B(4,0).

(1)求抛物线的解析式;
(2)若点M是抛物线上的一动点,且在直线BC的上方,当S△MBC取得最大值时,求点M的坐标;
(3)在直线的上方,抛物线是否存在点M,使四边形ABMC的面积为15?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家电销售商店1-6周销售甲、乙两种品牌冰箱的数量如图所示(单位:台):
(1)分别求该商店这段时间内甲、乙两种品牌冰箱周销售量的平均数和方差;
(2)根据计算结果及折线统计图,对该商店今后采购这两种品牌冰箱的意向提出建议,并说明理由.
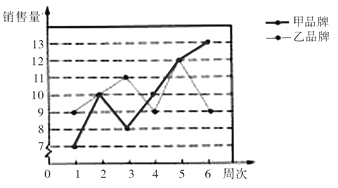
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1 ,它与x轴交于两点O,A;将C1绕点A旋转180°得到C2 , 交x轴于A1;将C2绕点A1旋转180°得到C3 , 交x轴于点A2 . .....如此进行下去,直至得到C2018 , 若点P(4035,m)在第2018段抛物线上,则m的值为________.
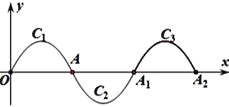
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com