
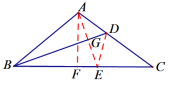
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,若
,若![]() ,
,![]() ,则线段
,则线段![]() 的长为________.
的长为________.
【答案】![]()
【解析】
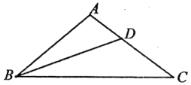
在BC上取一点E,使BE=AB,作AF⊥BC,连接AN交BD于点G,可证△ABD≌△EBD,根据全等三角形的性质,证得AE=EC,由线段垂直平分线的判定定理可知BD是线段AE的垂直平分线,进而求得BG的长,根据面积相等求得AF的长,再由勾股定理得出EF、AC的长;再等高的三角形的面积比等于底边的比求得CD的长.
解:在BC上取一点E,使BE=AB,作AF⊥BC,连接AN交BD于点G,
∵BD平分∠ABC,
∴∠ABD=∠CBD,BD=BD,AB=BE=6![]()
∴△ABD≌△EBD
∴AD=DE,∠BAE=∠BEA=∠EAD+∠C,
∴∠BAC=∠BAE+∠EAC=∠EAD+∠C+∠EAC=2∠EAC+∠C
又∵∠BAC=3∠C
∴2∠EAC+∠C=3∠C
∴∠EAC=∠C∴AE=EC
∵AB=6![]() ,BC=10
,BC=10![]() ,
,
∴EC=4![]() =AE
=AE
∵AB=BE,AD=DE
∴BD是AE的垂直平分线,
∴AG=2![]()
∴BG=![]()
根据面积相等,得![]() ,即
,即![]()
∴AF=![]()
∴EF=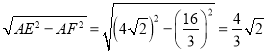
∴CF=CE+EF=4![]() +
+![]() =
=![]()
∴AC=![]()
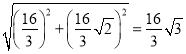
∵S△ADB=S△EDB
∴![]()
∴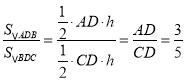
∴![]()


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=10,BC=15,点D,E,P分别是边AC,AB;BC上的点,且AD=4,AE=4EB.若![]() 是等腰三角形,则CP的长是__________.
是等腰三角形,则CP的长是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自我省深化课程改革以来,某校开设了:A.利用影长求物体高度,B.制作视力表,C.设计遮阳棚,D.制作中心对称图形,四类数学实践活动课.规定每名学生必选且只能选修一类实践活动课,学校对学生选修实践活动课的情况进行抽样调查,将调查结果绘制成如下两幅不完整的统计图.
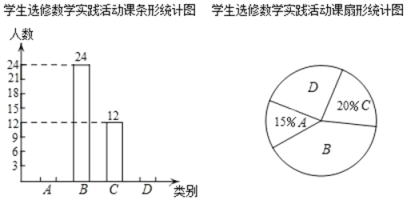
根据图中信息解决下列问题:
(1)本次共调查名学生,扇形统计图中B所对应的扇形的圆心角为度;
(2)补全条形统计图;
(3)选修D类数学实践活动的学生中有2名女生和2名男生表现出色,现从4人中随机抽取2人做校报设计,请用列表或画树状图法求所抽取的两人恰好是1名女生和1名男生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】使用家用燃气灶烧开同一壶水所需的燃气量![]() (单位:
(单位:![]() )与旋钮的旋转角度
)与旋钮的旋转角度![]() (单位:度)(
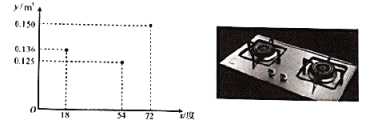
(单位:度)(![]() )近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度
)近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度![]() 与燃气量
与燃气量![]() 的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )
的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
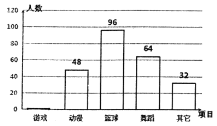
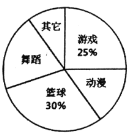
【题目】某地区对学生业余爱好进行抽样调查,被抽取的同学每人在下面五项:“游戏”,“动漫”,“篮球”,“舞蹈”“其它”中选一项最喜欢的活动,并将调查结果绘制成以下两幅不完整的统计图,请根据图中的信息,解答下列问题:
(1)这次抽样调查中,一共抽查了多少名学生?
(2)请补全条形统计图;
(3)根据调查结果,估计该地区5000名学生中有多少人最喜欢“舞蹈”.
查看答案和解析>>
科目:初中数学 来源: 题型:
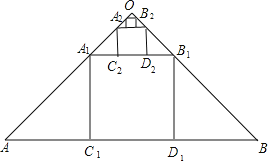
【题目】如图,在斜边长为1的等腰直角三角形OAB中,作内接正方形A1B1C1D1;在等腰直角三角形OA1B1中,作内接正方形A2B2C2D2;在等腰直角三角形OA2B2中,作内接正方形A3B3C3D3;……;依次作下去,则第n个正方形AnBnCnDn的边长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
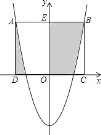
【题目】已知二次函数y=2x2+m.(1)若点(-2,y1)与(3,y2)在此二次函数的图象上,则y1_________y2(填“>”、“=”或“<”);(2)如图,此二次函数的图象经过点(0,-4),正方形ABCD的顶点C、D在x轴上,A、B恰好在二次函数的图象上,求图中阴影部分的面积之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,甲、乙两城决定向![]() 、
、![]() 两乡运送肥料以支持农村生产,已知甲、乙两城共有肥料800吨,其中乙城肥料是甲城的2倍少100吨,从甲城往
两乡运送肥料以支持农村生产,已知甲、乙两城共有肥料800吨,其中乙城肥料是甲城的2倍少100吨,从甲城往![]() 、
、![]() 两乡运肥料的费用分别为20元吨和25元吨;从乙城往
两乡运肥料的费用分别为20元吨和25元吨;从乙城往![]() 、
、![]() 两乡运肥料的费用分别为15元吨和26元吨.现
两乡运肥料的费用分别为15元吨和26元吨.现![]() 乡需要肥料440吨,
乡需要肥料440吨,![]() 乡需要肥料360吨.
乡需要肥料360吨.
(1)甲城和乙城各有多少吨肥料?
(2)设从甲城运往![]() 乡肥料
乡肥料![]() 吨,总运费为
吨,总运费为![]() 元,求出最少总运费.
元,求出最少总运费.
(3)由于更换车型,使甲城运往![]() 乡的运费每吨减少
乡的运费每吨减少![]() 元,这时从甲城运往
元,这时从甲城运往![]() 乡肥料多少吨才能使总运费最少,最少是多少?
乡肥料多少吨才能使总运费最少,最少是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
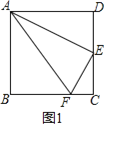
【题目】如图1,在正方形![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 边上一点,且
边上一点,且![]() .
.
(1)求证:![]() ;
;
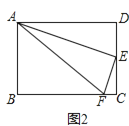
(2)将“正方形”改成“矩形”,其他条件均不变,如图2,你认为仍然有“![]() ”吗?若你同意,请以图2为例加以证明;若你不同意,请说明理由.
”吗?若你同意,请以图2为例加以证明;若你不同意,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com