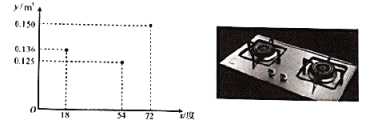
【题目】使用家用燃气灶烧开同一壶水所需的燃气量
（单位：
）与旋钮的旋转角度
（单位：度）（
）近似满足函数关系y=ax2+bx+c(a≠0).如图记录了某种家用燃气灶烧开同一壶水的旋钮角度与燃气量的三组数据，根据上述函数模型和数据，可推断出此燃气灶烧开一壶水最节省燃气的旋钮角度约为（ ）
A. 
B. 
C. 
D. 
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】2017年10月18日，党的十九大报告提出“乡村振兴”战略，之后各地发展乡村旅游，某村在2018年3月1日首次举办“百花节”，开园免费赏花，于是大批游客涌入该村赏花，吃农家饭买土特产，平均每人消费100元．
（1）据统计，某个周六早上开园后平均每小时有500人进园，两小时后，平均每小时有100人离园，园区规定，当园区内游客人数达到3000时，将停止进园，那么从开园起经过多少小时后停止进园？
（2）该村对园区加大建设和宣传力度，2019年3月1日，第二届“百花节”如期开园，同时规定进园门票费为每人60元，受各种因素影响，与2018年同期相比，人数在20000的基础上降低了a%，除门票外平均每人消费金额增长了
a%，园区总收入增长了
a%，求a的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】二次函数 y＝ax2+bx+c（a≠0）的图象如图所示，对称轴是直线 x＝1，下列结论：①ab＜0；②b2＞4ac；③a+b+2c＜0；④3a+c＜0． 其中正确的是（ ）
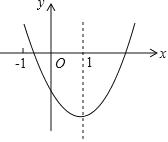
A.①④B.②④C.①②③D.①②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某宾馆有50个房间供游客居住，当每个房间定价120元时，房间会全部住满，当每个房间每天的定价每增加10元时，就会有一个房间空闲。如果游客居住房间，宾馆需对每个房间每天支出20元的各种费用，设每个房间定价增加10 x元（x为整数）。
（1）（2分）直接写出每天游客居住的房间数量y与x的函数关系式。
（2）（4分）设宾馆每天的利润为W元，当每间房价定价为多少元时，宾馆每天所获利润最大，最大利润是多少？
（3）（4分）某日，宾馆了解当天的住宿的情况，得到以下信息：①当日所获利润不低于5000元，②宾馆为游客居住的房间共支出费用没有超过600元，③每个房间刚好住满2人。问：这天宾馆入住的游客人数最少有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数
分别交y轴、x轴于A、B两点，抛物线y=﹣x2+bx+c过A、B两点．
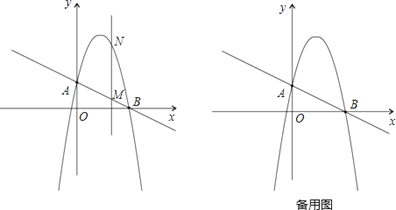
（1）求这个抛物线的解析式；
（2）作垂直x轴的直线x=t，在第一象限交直线AB于M，交这个抛物线于N．求当t取何值时，MN有最大值？最大值是多少？
（3）在（2）的情况下，以A、M、N、D为顶点作平行四边形，求第四个顶点D的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
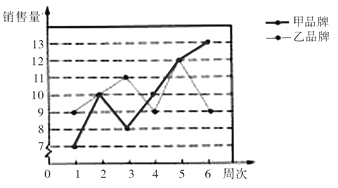
【题目】某家电销售商店1-6周销售甲、乙两种品牌冰箱的数量如图所示（单位：台）：
（1）分别求该商店这段时间内甲、乙两种品牌冰箱周销售量的平均数和方差；
（2）根据计算结果及折线统计图，对该商店今后采购这两种品牌冰箱的意向提出建议，并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
