
����Ŀ����ͼ��������y��ax2+bx��a��0������E��8��0��������ABCD�ı�AB���߶�OE�ϣ���A�ڵ�B����ࣩ����C��D���������ϣ���BAD��ƽ����AM��BC�ڵ�M����N��CD���е㣬��֪OA��2����OA��AD��1��3.
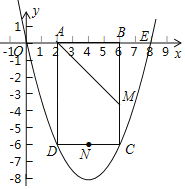
��1���������ߵĽ���ʽ��
��2��F��G�ֱ�Ϊx�ᣬy���ϵĶ��㣬˳������M��N��G��F�����ı���MNGF�����ı���MNGF�ܳ�����Сֵ��
��3����x���·��������������Ƿ���ڵ�P��ʹ��ODP��OD���ϵĸ�Ϊ![]() �������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��4������ABCD������������������ƽ�ƣ���ƽ�ƺ������������εı�����������K��L����ֱ��KLƽ�־��ε����ʱ����������ƽ�Ƶľ���.
���𰸡���1��y��![]() x2��4x����2���ı���MNGF�ܳ���СֵΪ12
x2��4x����2���ı���MNGF�ܳ���СֵΪ12![]() ����3�����ڵ�P��P����Ϊ��6����6������4��������ƽ�Ƶľ���Ϊ3����λ����.
����3�����ڵ�P��P����Ϊ��6����6������4��������ƽ�Ƶľ���Ϊ3����λ����.
��������
��1���ɵ�E��x���������ҵ�A���߶�OE�ϵõ���A��x���������ϣ�����A��2��0������OA��2����OA��AD��1��3��AD��6.�����ı���ABCDΪ���Σ�����AD��AB�����Ե�D�ڵ������ޣ���������A�ĺ�������ͬ�������õ���D����.�������߾�����D��E���ô���ϵ��������������ʽ����2�������ı���MNGF�����ڵ�F��G�ֱ���x�ᡢy�����˶����ʿ�����M����x��ĶԳƵ��M'������N����y��ĶԳƵ��N'����FM��FM'��GN��GN'.�õ�M'��F��G��N'��ͬһֱ����ʱN'G+GF+FM'��M'N'��С�����ı���MNGF�ܳ���Сֵ����MN+M'N'.���ݾ������ʡ������������ʵ����������M��M'��N��N'���꣬����ô𰸣���3����ΪOD��������֪��ODP��OD���ϵĸߣ��ʿ����ODP�����.����Ϊ��ODP������������ǹ���P��PQƽ��y�ύֱ��OD�ڵ�Q���ѡ�ODP���Ϊ��OPQ���DPQ�ĺͻ�������㣬�ʴ��ڵ�����ϵ.���P����Ϊt����t��ʾPQ�ij������з���.���t��ֵҪ�����Ƿ������P��x���·�����������4����KLƽ�־���ABCD������ɵ�K���߶�AB�ϡ�L���߶�CD�ϣ�����ƽ�ƺ�������߿�֪����K�ɵ�Oƽ�Ƶõ�����L�ɵ�Dƽ�Ƶõ�������K��m��0����L��2+m��-6��.��֤KLƽ�־������ʱ��KLһ���������ε�����H�ұ�Hƽ�֣����H����Ϊ��4����3�������е����깫ʽ�����m��ֵ.
��1���ߵ�A���߶�OE�ϣ�E��8��0����OA��2
��A��2��0��
��OA��AD��1��3
��AD��3OA��6
���ı���ABCD�Ǿ���
��AD��AB
��D��2����6��
��������y��ax2+bx������D��E
��![]()
��ã�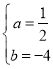
�������ߵĽ���ʽΪy��![]() x2��4x
x2��4x
��2����ͼ1������M����x��ĶԳƵ�M'������N����y��ĶԳƵ�N'������FM'��GN'��M'N'
��y��![]() x2��4x��
x2��4x��![]() ��x��4��2��8
��x��4��2��8
�������߶Գ���Ϊֱ��x��4
�ߵ�C��D���������ϣ���CD��x�ᣬD��2����6��
��yC��yD����6������C��D����ֱ��x��4�Գ�
��xC��4+��4��xD����4+4��2��6����C��6����6��
��AB��CD��4��B��6��0��
��AMƽ�֡�BAD����BAD����ABM��90��
���BAM��45��
��BM��AB��4
��M��6����4��
�ߵ�M��M'����x��Գƣ���F��x����
��M'��6��4����FM��FM'
��NΪCD�е�
��N��4����6��
�ߵ�N��N'����y��Գƣ���G��y����
��N'����4����6����GN��GN'
��C�ı���MNGF��MN+NG+GF+FM��MN+N'G+GF+FM'
�ߵ�M'��F��G��N'��ͬһֱ����ʱ��N'G+GF+FM'��M'N'��С
��C�ı���MNGF��MN+M'N'=![]()
���ı���MNGF�ܳ���СֵΪ12![]() .
.
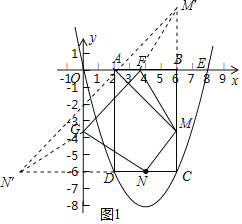
��3�����ڵ�P��ʹ��ODP��OD���ϵĸ�Ϊ![]() .
.
����P��PQ��y�ύֱ��OD�ڵ�Q
��D��2����6��
��OD��![]() ��ֱ��OD����ʽΪy����3x
��ֱ��OD����ʽΪy����3x
���P������t��![]() t2��4t����0��t��8�������Q��t����3t��
t2��4t����0��t��8�������Q��t����3t��
����ͼ2����0��t��2ʱ����P�ڵ�D���

��PQ��yQ��yP����3t����![]() t2��4t������
t2��4t������![]() t2+t
t2+t
��S��ODP��S��OPQ+S��DPQ��![]() PQxP+
PQxP+![]() PQ��xD��xP����
PQ��xD��xP����![]() PQ��xP+xD��xP����
PQ��xP+xD��xP����![]() PQxD��PQ����
PQxD��PQ����![]() t2+t
t2+t
�ߡ�ODP��OD���ϵĸ�h��![]() ��
��
��S��ODP��![]() ODh
ODh
�ੁ![]() t2+t��
t2+t��![]() ��2
��2![]() ��
��![]()
������
����ͼ3����2��t��8ʱ����P�ڵ�D�Ҳ�
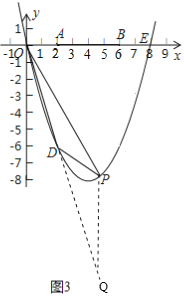
��PQ��yP��yQ��![]() t2��4t������3t����
t2��4t������3t����![]() t2��t
t2��t
��S��ODP��S��OPQ��S��DPQ��![]() PQxP��
PQxP��![]() PQ��xP��xD����
PQ��xP��xD����![]() PQ��xP��xP+xD����
PQ��xP��xP+xD����![]() PQxD��PQ��
PQxD��PQ��![]() t2��t
t2��t
��![]() t2��t��
t2��t��![]() ��2
��2![]() ��
��![]()
��ã�t1����4����ȥ����t2��6
��P��6����6��
������������P����Ϊ��6����6������ʹ��ODP��OD���ϵĸ�Ϊ![]() .
.
��4��������������ƽ��m����λ���Ⱥ������ABCD�н���K��L
��KLƽ�־���ABCD�����
��K���߶�AB�ϣ�L���߶�CD�ϣ���ͼ4
��K��m��0����L��2+m��-6��
����AC����KL�ڵ�H ��S��ACD��S�ı���ADLK�� ��S��AHK��S��CHL ��AK��LC ���AHK�ס�CHL �� ��AH��CH��KH=HL������HΪAC�е㣬Ҳ��KL�е� ��H��4����3�� �� ��m��3 ��������ƽ�Ƶľ���Ϊ3����λ����.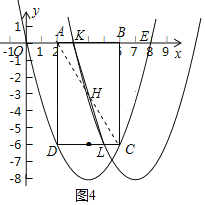
![]() S����ABCD
S����ABCD =
=![]() =1��
=1��![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx+c��a��0����y�ύ�ڵ�C��0��4������x�ύ��A����2��0������B��4��0����

��1���������ߵĽ���ʽ��
��2������M���������ϵ�һ���㣬����ֱ��BC���Ϸ�����S��MBCȡ�����ֵʱ�����M�����ꣻ
��3����ֱ�ߵ��Ϸ����������Ƿ���ڵ�M��ʹ�ı���ABMC�����Ϊ15�������ڣ������M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��ֱ������
��ֱ������![]() ��
��![]() ��һ�㣬��
��һ�㣬��![]() ��
��![]() ���е㣬����
���е㣬����![]() ��
��![]() �����ߣ���
�����ߣ���![]() ��
��![]() ���ӳ��߷ֱ��ڵ�
���ӳ��߷ֱ��ڵ�![]() ��
��![]() ������
������![]() ��
��

��1����֤��![]() ��
��
��2����գ�
����֪![]() ����
����![]() _________ʱ��
_________ʱ��![]() ��
��
������![]() ��
��![]() ��
��![]() ����
����![]() �Ķ���Ϊ_________ʱ���ı���
�Ķ���Ϊ_________ʱ���ı���![]() �����Σ�
������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
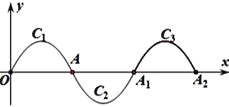
����Ŀ����ͼ��һ�������ߣ�y=-x(x-2)��0��x��2����ΪC1 ,����x�ύ������O��A����C1�Ƶ�A��ת180���õ�C2 �� ��x����A1����C2�Ƶ�A1��ת180���õ�C3 �� ��x���ڵ�A2 �� ������������˽�����ȥ��ֱ���õ�C2018 �� ����P��4035��m���ڵ�2018���������ϣ���m��ֵΪ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
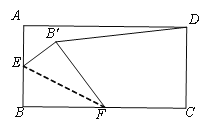
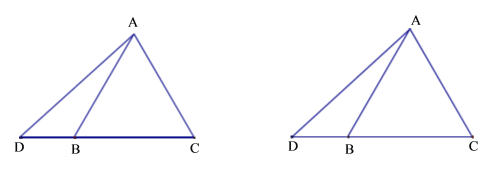
����Ŀ����ͼ������ABCD�У�AD��4��AB��2����E��AB���е㣬��F��BC���ϵ�����һ�㣨����B��C�غϣ�����EBF��EF���ۣ���B����B'������DB'�ij�����Сʱ��BF�ij���Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������Ƶġ���һ���ǵ�����֪�ǡ��ij߹���ͼ���̣�
��֪��RT��ABC��
������AB������D��ʹ��BCD=��A��

��������ͼ����ACΪֱ����Բ����AB��D�����Ե�D�����������ĵ㣻
����������Ƶ���ͼ���̣���������֤����
֤������AC��ֱ��
���ADC=90����______���������������ݣ�
����ACD+��A=90����
�ߡ�ACB=90����
����ACD+_______=90����
���BCD=��A��_______���������������ݣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
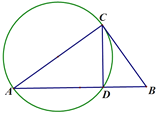
����Ŀ����ͼ���ڵȱߡ�ABC�У���D �DZ�CB�ӳ�����һ����(BD<BC)������AD����B ����ֱ��AD�ĶԳƵ�ΪE����D ��DF//AB��CE�ڵ�F��
��1�������ⲹȫͼ�Σ�
��2����֤��AD=CF��
��3������DCE=15��ʱ��ֱ��д���߶�AD��EF��BC֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB��AC����ABΪֱ������O��BC�ڵ�D������D��AC�Ĵ��߽�AC�ڵ�E����AB���ӳ����ڵ�F��
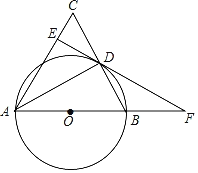
��1����֤��DE����O���У�
��2����CD��BF��AE��3����DF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
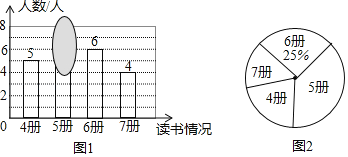
����Ŀ����ʦ�������˱�ѧ��ѧ�����������������������Ƴ�����ͼ��ͼ1���Ͳ�����������ͼ��ͼ2������������ͼ��ī���ڸ���һ���֣�
��1��������ͼ�б��ڸǵ�������д����������λ����
��2����������ѧ�������ѡһ��̸������룬��ѡ�ж��鳬��5���ѧ���ĸ��ʣ�
��3������ֲ��������⼸�ˣ���֪���ٵĶ���6�ᣬ������֮ǰ�����ݺϲ����ֲ�������λ��û�ı䣬����ಹ������ ���ˣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com