
����Ŀ����ʦ�������˱�ѧ��ѧ�����������������������Ƴ�����ͼ��ͼ1���Ͳ�����������ͼ��ͼ2������������ͼ��ī���ڸ���һ���֣�
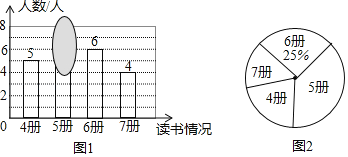
��1��������ͼ�б��ڸǵ�������д����������λ����
��2����������ѧ�������ѡһ��̸������룬��ѡ�ж��鳬��5���ѧ���ĸ��ʣ�
��3������ֲ��������⼸�ˣ���֪���ٵĶ���6�ᣬ������֮ǰ�����ݺϲ����ֲ�������λ��û�ı䣬����ಹ������ ���ˣ�
���𰸡���1������ͼ�б��ڸǵ���Ϊ9����������λ��Ϊ5����2��ѡ�ж��鳬��5���ѧ���ĸ���Ϊ![]() ����3��3
����3��3
����������1���ö���Ϊ6���������������ռ�İٷֱȵõ�������������������������ֱ��ȥ����Ϊ4�ᡢ6���7��������õ�����5���������Ȼ�������λ���Ķ������������λ����
��2���ö���Ϊ6���7��������ͳ����������õ�ѡ�ж��鳬��5���ѧ���ĸ��ʣ�
��3��������λ���Ķ�����ж����������ܳ���27���Ӷ��õ���ಹ���������
��1������ѧ������Ϊ6��25%=24���ˣ���
����Ϊ5���ѧ����Ϊ24��5��6��4=9���ˣ���
��������ͼ�б��ڸǵ���Ϊ9����������λ��Ϊ5��
��2��ѡ�ж��鳬��5���ѧ���ĸ���=![]() ��
��
��3����Ϊ4���5���������Ϊ14����λ��û�ı䣬�������������ܳ���27������ಹ����3�ˣ�
�ʴ�Ϊ��3��


 �߲������Ӧ��һ��ͨϵ�д�
�߲������Ӧ��һ��ͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y��ax2+bx��a��0������E��8��0��������ABCD�ı�AB���߶�OE�ϣ���A�ڵ�B����ࣩ����C��D���������ϣ���BAD��ƽ����AM��BC�ڵ�M����N��CD���е㣬��֪OA��2����OA��AD��1��3.
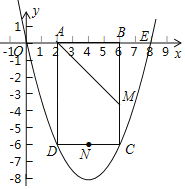
��1���������ߵĽ���ʽ��
��2��F��G�ֱ�Ϊx�ᣬy���ϵĶ��㣬˳������M��N��G��F�����ı���MNGF�����ı���MNGF�ܳ�����Сֵ��
��3����x���·��������������Ƿ���ڵ�P��ʹ��ODP��OD���ϵĸ�Ϊ![]() �������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��4������ABCD������������������ƽ�ƣ���ƽ�ƺ������������εı�����������K��L����ֱ��KLƽ�־��ε����ʱ����������ƽ�Ƶľ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������м��أ������м��Ҷ��˳�Ǯ��֪���������Ұ��Ǯ��ʮ���ҵü�̫���Ǯ����ʮ���ʼס��ҳ�Ǯ�����Σ������ģ������м��Ҷ��ˣ���֪��Ǯ�����ж���Ǯ�����Ұ��Լ�һ���Ǯ���ף����Ǯ��Ϊ50Ǯ�����װ��Լ�![]() ��Ǯ���ң����ҵ�Ǯ��ҲΪ50Ǯ���ʼס��Ҹ��ж���Ǯ������ס���ԭ��Ǯ���ֱ�Ϊ
��Ǯ���ң����ҵ�Ǯ��ҲΪ50Ǯ���ʼס��Ҹ��ж���Ǯ������ס���ԭ��Ǯ���ֱ�Ϊ![]() ��
��![]() ���������з�������ȷ���ǣ� ��
���������з�������ȷ���ǣ� ��
A.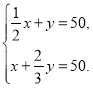 B.
B.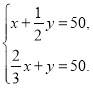 C.
C.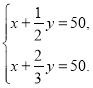 D.
D.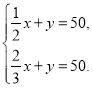
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
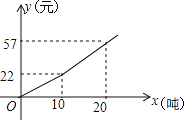
����Ŀ��Ϊ���������Լ��ˮ��ij������ˮ��˾���ֶ��շѱ��շѣ���ͼ��ӳ����ÿ����ˮ��y��Ԫ������ˮ��x���֣�֮��ĺ�����ϵ
��1��С������·���ˮ8�֣�Ӧ��ˮ��_____Ԫ��
��2���������ֶ��շѱ���С����������·ݷֱ�ˮ��36Ԫ��19.8Ԫ�������·ݱ����·ݽ�Լ��ˮ���ٶ֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲���룺
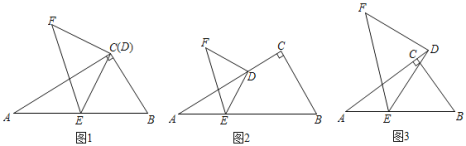
��1����ͼ1����Rt��ABC�У���ACB��90������BAC��30������D���C�غϣ���E��б��AB�ϣ�����DE����DE��AE�����߶�DE�Ƶ�D˳ʱ����ת90���õ��߶�DF������EF����![]() ��______��sin��ADE��________��
��______��sin��ADE��________��
̽��֤����
��2���ڣ�1���У��������D��CA�����ƶ���ʹCD��![]() AC�������������䣬��ͼ2�����������Ƿֲ��䣿���ı䣬�����������ֵ�������䣬��˵�����ɣ�
AC�������������䣬��ͼ2�����������Ƿֲ��䣿���ı䣬�����������ֵ�������䣬��˵�����ɣ�
��չ����
��3����ͼ3���ڡ�ABC�У���ACB��90������CAB��a����D�ڱ�AC���ӳ����ϣ�E��AB������һ�㣬����DE��ED��nAE�����߶�DE���ŵ�D˳ʱ����ת90������F������EF����![]() ��sin��ADE��ֵ�ֱ��Ƕ��٣������ú���n��a��ʽ�ӱ�ʾ��
��sin��ADE��ֵ�ֱ��Ƕ��٣������ú���n��a��ʽ�ӱ�ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������ȷ���ǣ� ��
A.ͬһƽ���ڣ���һ������ֻ��һ��ֱ������ֱ֪��ƽ��
B.���ŷֱ������Ρ��ȱ������Ρ�Բ�Ŀ�Ƭ�����������ȡһ�ţ�ǡ�ó鵽���ĶԳ�ͼ�ο�Ƭ�ĸ�����![]()
C.һ��Ա�ƽ�У�һ��Ա���ȵ��ı�����ƽ���ı���
D.��![]() ʱ������
ʱ������![]() �ķ���
�ķ���![]() ��ʵ����
��ʵ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
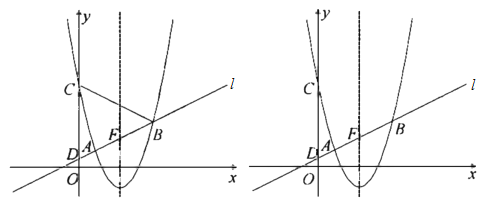
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У���ֱ��
�У���ֱ��![]() Ϊ�Գ����������
Ϊ�Գ����������![]() ��ֱ��
��ֱ��![]() ����
����![]() ��
��![]() ���㣬��
���㣬��![]() �ύ��
�ύ��![]() ��ֱ��
��ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() .
.
��1���������ߵĺ�������ʽ��
��2����ֱ��![]() �������ߵĶԳ���Ľ���Ϊ
�������ߵĶԳ���Ľ���Ϊ![]() ��
��![]() ����������λ�ڶԳ����Ҳ��һ�㣬��
����������λ�ڶԳ����Ҳ��һ�㣬��![]() ����
����![]() ��
��![]() �������ȣ����
�������ȣ����![]() �����ꣻ
�����ꣻ
��3������![]() ��������ֻ��һ��
��������ֻ��һ��![]() ��ʹ
��ʹ![]() ����
����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У���
����![]() ��
��![]() ��
��![]() �����DZ�
�����DZ�![]() ���ĵȷֵ㣬��
���ĵȷֵ㣬��![]() ��
��![]() ��
��![]() �����DZ�
�����DZ�![]() ���ĵȷֵ㣬�ֱ���
���ĵȷֵ㣬�ֱ���![]() ��
��![]() ��
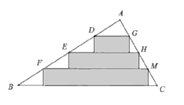
��![]() Ϊ�����¼���������ȵľ��Σ���ͼ��ʾ����ͼ�пհײ��ֵ������Ϊ
Ϊ�����¼���������ȵľ��Σ���ͼ��ʾ����ͼ�пհײ��ֵ������Ϊ![]() ����ͼ����Ӱ���ֵ�������ǣ� ��
����ͼ����Ӱ���ֵ�������ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��ax2+bx+c��a��0����x�ύ�ڵ�A����1��0������y��Ľ����ڣ�0��2������0��3��֮�䣨�����˵㣩����������Ϊ��1��n���������н��ۣ�
��4a+2b��0��
�ک�1��a��![]() ��
��
����������ʵ��m��a+b��am2+bm�ܳ�����
������x�ķ���ax2+bx+c��n��1����������ȵ�ʵ������
���н�����ȷ�ĸ���Ϊ��������
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com