
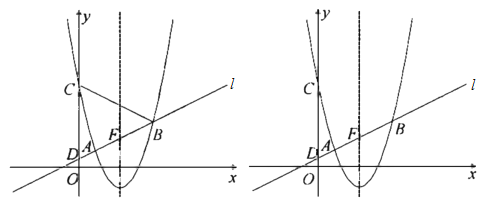
【题目】如图,在平面直角坐标系![]() 中,以直线
中,以直线![]() 为对称轴的抛物线
为对称轴的抛物线![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于
轴交于![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的函数表达式;
(2)设直线![]() 与抛物线的对称轴的交点为
与抛物线的对称轴的交点为![]() ,
,![]() 是抛物线上位于对称轴右侧的一点,若
是抛物线上位于对称轴右侧的一点,若![]() ,且
,且![]() 与
与![]() 的面积相等,求点
的面积相等,求点![]() 的坐标;
的坐标;
(3)若在![]() 轴上有且只有一点
轴上有且只有一点![]() ,使
,使![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() .;(2)点
.;(2)点![]() 坐标为
坐标为![]() ;
;![]() .(3)
.(3)![]() .
.
【解析】(1)根据已知列出方程组求解即可;
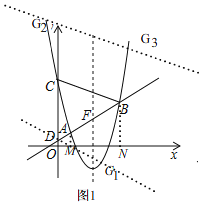
(2)作AM⊥x轴,BN⊥x轴,垂足分别为M,N,求出直线l的解析式,再分两种情况分别求出G点坐标即可;
(3)根据题意分析得出以AB为直径的圆与x轴只有一个交点,且P为切点,P为MN的中点,运用三角形相似建立等量关系列出方程求解即可.
(1)由题可得: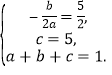 解得
解得![]() ,
,![]() ,
,![]() .
.
![]() 二次函数解析式为:
二次函数解析式为:![]() .
.
(2)作![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() ,则
,则![]() .
.
![]() ,
,![]() ,
,![]() ,
,
 ,解得
,解得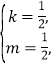 ,
,![]() ,
,![]() .
.
同理,![]() .
.
![]() ,
,
![]() ①
①![]() (
(![]() 在
在![]() 下方),
下方),![]() ,
,
![]() ,即
,即![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() .
.
②![]() 在
在![]() 上方时,直线
上方时,直线![]() 与
与![]() 关于
关于![]() 对称.
对称.
![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() .
.
综上所述,点![]() 坐标为
坐标为![]() ;
;![]() .
.
(3)由题意可得:![]() .
.
![]() ,
,![]() ,
,![]() ,即
,即![]() .
.
![]() ,
,![]() ,
,![]() .
.
设![]() 的中点为
的中点为![]() ,
,
![]() 点有且只有一个,
点有且只有一个,![]() 以
以![]() 为直径的圆与
为直径的圆与![]() 轴只有一个交点,且
轴只有一个交点,且![]() 为切点.
为切点.
![]() 轴,
轴,![]() 为
为![]() 的中点,
的中点,![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,![]() .
.
![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】(感知)如图①在等边△ABC和等边△ADE中,连接BD,CE,易证:△ABD≌△ACE;
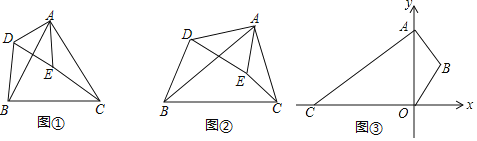
(探究)如图②△ABC与△ADE中,∠BAC=∠DAE,∠ABC=∠ADE,求证:△ABD∽△ACE;
(应用)如图③,点A的坐标为(0,6),AB=BO,∠ABO=120°,点C在x轴上运动,在坐标平面内作点D,使AD=CD,∠ADC=120°,连结OD,则OD的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB=AC,AD为∠BAC的角平分线,D、E、F…为∠BAC的角平分线上的若干点.如图1,连接BD、CD,图中有1对全等三角形;如图2,连接BD、CD、BE、CE,图中有3对全等三角形;如图3,连接BD、CD、BE、CE、BF、CF,图中有6对全等三角形;依此规律,第n个图形中有_____对全等三角形.
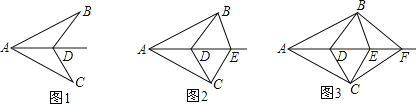
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC,(1)如图①,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+![]() ∠A;(2)如图②,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图③,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-
∠A;(2)如图②,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图③,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-![]() ∠A.上述说法正确的个数是( )
∠A.上述说法正确的个数是( )

A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了给游客提供更好的服务,某景区随机对部分游客进行了关于“景区服务工作满意度”的调查,并根据调查结果绘制成如下不完整的统计图表.
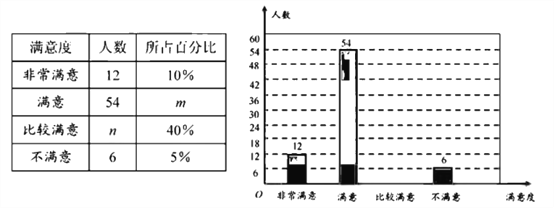
根据图表信息,解答下列问题:
(1)本次调查的总人数为 ,表中![]() 的值为 ;
的值为 ;
(2)请补全条形统计图;
(3)据统计,该景区平均每天接待游客约3600人,若将“非常满意”和“满意”作为游客对景区服务工作的肯定,请你估计该景区服务工作平均每天得到多少名游客的肯定.
查看答案和解析>>
科目:初中数学 来源: 题型:
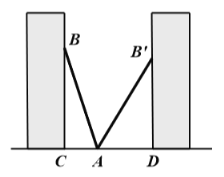
【题目】如图,小巷左右两侧是竖直的墙,一架梯子![]() 斜靠在左墙时,梯子底端到左墙角的距离
斜靠在左墙时,梯子底端到左墙角的距离![]() 为0.7米,顶端到地面距离
为0.7米,顶端到地面距离![]() 为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端到地面距离
为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端到地面距离![]() 为2米,求小巷的宽度
为2米,求小巷的宽度![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列多面体,并把下表补充完整.
名称 | 三棱柱 | 四棱柱 | 五棱柱 | 六棱柱 |
图形 |
|
|
|
|
顶点数 | 6 | 10 | 12 | |
棱数 | 9 | 12 | ||
面数 | 5 | 8 |
观察上表中的结果,你能发现![]() 、
、![]() 、
、之间有什么关系吗?请写出关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com