
【题目】如图,在等腰三角形△ABC中,O为底边BC的中点,以O为圆心作半圆与AB,AC相切,切点分别为D,E.过半圆上一点F作半圆的切线,分别交AB,AC于M,N.那么![]() 的值等于( )
的值等于( )
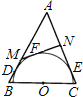
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
分别交y轴、x轴于A、B两点,抛物线y=﹣x2+bx+c过A、B两点.
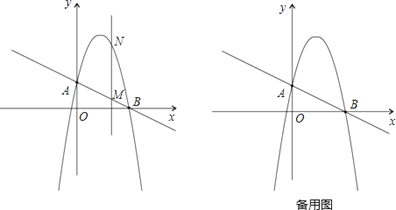
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于M,交这个抛物线于N.求当t取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
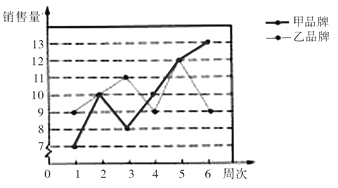
【题目】某家电销售商店1-6周销售甲、乙两种品牌冰箱的数量如图所示(单位:台):
(1)分别求该商店这段时间内甲、乙两种品牌冰箱周销售量的平均数和方差;
(2)根据计算结果及折线统计图,对该商店今后采购这两种品牌冰箱的意向提出建议,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
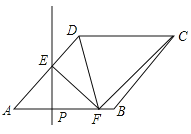
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一动点,且不与点
上一动点,且不与点![]() 重合,过点
重合,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,将
,将![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在直线
落在直线![]() 上点
上点![]() 处,连接
处,连接![]() 、
、![]() ,当
,当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长是_________.
的长是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 是
是![]() 上一点,点
上一点,点![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 的切线,与
的切线,与![]() 、
、![]() 的延长线分别交于点
的延长线分别交于点![]() 、
、![]() ,连接
,连接![]() .
.

(1)求证:![]() .
.
(2)填空:
①已知![]() ,当
,当![]() _________时,
_________时,![]() .
.
②连接![]() 、
、![]() 、
、![]() .当
.当![]() 的度数为_________时,四边形
的度数为_________时,四边形![]() 是菱形.
是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
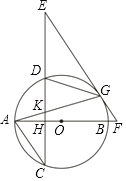
【题目】如图,AB是⊙O的直径,过圆外一点E作EF与⊙O相切于G,交AB的延长线于F,EC⊥AB于H,交⊙O于D,C两点,连接AG交DC于K.
(1)求证:EG=EK;
(2)连接AC,若AC∥EF,cosC=![]() ,AK=
,AK=![]() ,求BF的长.
,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
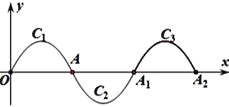
【题目】如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1 ,它与x轴交于两点O,A;将C1绕点A旋转180°得到C2 , 交x轴于A1;将C2绕点A1旋转180°得到C3 , 交x轴于点A2 . .....如此进行下去,直至得到C2018 , 若点P(4035,m)在第2018段抛物线上,则m的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
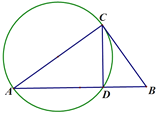
【题目】下面是娜娜设计的“作一个角等于已知角”的尺规作图过程.
已知:RT△ABC,
求作:AB上作点D,使∠BCD=∠A.

作法:如图,以AC为直径作圆,交AB于D,所以点D就是所求作的点;
根据娜娜设计的作图过程,完成下面的证明.
证明:∵AC是直径
∴∠ADC=90°(______)(填推理的依据)
即∠ACD+∠A=90°,
∵∠ACB=90°,
即∠ACD+_______=90°,
∴∠BCD=∠A(_______)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别加工100个零件,甲第1个小时加工了10个零件,之后每小时加工30个零件.乙在甲加工前已经加工了40个零件,在甲加工3小时后乙开始追赶甲,结果两人同时完成任务.设甲、乙两人各自加工的零件数为![]() (个),甲加工零件的时间为
(个),甲加工零件的时间为![]() (时),
(时),![]() 与
与![]() 之间的函数图象如图所示.
之间的函数图象如图所示.

(1)在乙追赶甲的过程中,求乙每小时加工零件的个数.
(2)求甲提高加工速度后甲加工的零件数![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)当甲、乙两人相差12个零件时,直接写出甲加工零件的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com