
”¾ĢāÄæ”æ¼×”¢ŅŅĮ½ČĖ·Ö±š¼Ó¹¤100øöĮć¼ž£¬¼×µŚ1øöŠ”Ź±¼Ó¹¤ĮĖ10øöĮć¼ž£¬Ö®ŗóĆ抔Ź±¼Ó¹¤30øöĮć¼ž£®ŅŅŌŚ¼×¼Ó¹¤Ē°ŅŃ¾¼Ó¹¤ĮĖ40øöĮć¼ž£¬ŌŚ¼×¼Ó¹¤3Š”Ź±ŗóŅŅæŖŹ¼×·øĻ¼×£¬½į¹ūĮ½ČĖĶ¬Ź±Ķź³ÉČĪĪń£®Éč¼×”¢ŅŅĮ½ČĖø÷×Ō¼Ó¹¤µÄĮć¼žŹżĪŖ![]() £Øøö£©£¬¼×¼Ó¹¤Įć¼žµÄŹ±¼äĪŖ
£Øøö£©£¬¼×¼Ó¹¤Įć¼žµÄŹ±¼äĪŖ![]() £ØŹ±£©£¬
£ØŹ±£©£¬![]() Óė
Óė![]() Ö®¼äµÄŗÆŹżĶ¼ĻóČēĶ¼ĖłŹ¾£®
Ö®¼äµÄŗÆŹżĶ¼ĻóČēĶ¼ĖłŹ¾£®

£Ø1£©ŌŚŅŅ×·øĻ¼×µÄ¹ż³ĢÖŠ£¬ĒóŅŅĆ抔Ź±¼Ó¹¤Įć¼žµÄøöŹż£®
£Ø2£©Ēó¼×Ģįøß¼Ó¹¤ĖŁ¶Čŗó¼×¼Ó¹¤µÄĮć¼žŹż![]() Óė
Óė![]() Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£®
Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£®
£Ø3£©µ±¼×”¢ŅŅĮ½ČĖĻą²ī12øöĮć¼žŹ±£¬Ö±½ÓŠ“³ö¼×¼Ó¹¤Įć¼žµÄŹ±¼ä£®
”¾“š°ø”æ£Ø1£©ŌŚŅŅ×·øĻ¼×µÄ¹ż³ĢÖŠ£¬ŅŅĆ抔Ź±¼Ó¹¤Įć¼ž60øö£»£Ø2£©![]() £Ø
£Ø![]() £©£»£Ø3£©¼×¼Ó¹¤Įć¼žµÄŹ±¼äŹĒ
£©£»£Ø3£©¼×¼Ó¹¤Įć¼žµÄŹ±¼äŹĒ![]() Ź±”¢
Ź±”¢![]() Ź±»ņ
Ź±»ņ![]() Ź±
Ź±
”¾½āĪö”æ
£Ø1£©øł¾ŻĢāŅāæÉŅŌĒó³ö¼×ĖłÓĆŹ±¼ä£¬¼Ģ¶ųæÉµĆ³öŌŚŅŅ×·øĻ¼×µÄ¹ż³ĢÖŠ£¬ŅŅĆ抔Ź±¼Ó¹¤Įć¼žµÄøöŹż£»
£Ø2£©øł¾ŻĢāŅāŗĶŗÆŹżĶ¼ĻóÖŠµÄŹż¾ŻæÉŅŌĒó³ö¼×Ģįøß¼Ó¹¤ĖŁ¶Čŗó¼×¼Ó¹¤µÄĮć¼žŹż![]() Óė
Óė![]() Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£»
Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£»
£Ø3£©ĮŠŅ»ŌŖŅ»“Ī·½³ĢĒó½ā¼“æÉ£»
½ā£ŗ£Ø1£©¼×¼Ó¹¤100øöĮć¼žÓƵď±¼äĪŖ£ŗ![]() £ØŠ”Ź±£©£¬
£ØŠ”Ź±£©£¬
”ąŌŚŅŅ×·øĻ¼×µÄ¹ż³ĢÖŠ£¬ŅŅĆ抔Ź±¼Ó¹¤Įć¼žµÄøöŹżĪŖ£ŗ![]() £¬
£¬
“š£ŗŌŚŅŅ×·øĻ¼×µÄ¹ż³ĢÖŠ£¬ŅŅĆ抔Ź±¼Ó¹¤Įć¼ž60øö£»
£Ø2£©Éč¼×Ģįøß¼Ó¹¤ĖŁ¶Čŗó¼×¼Ó¹¤µÄĮć¼žŹż![]() Óė
Óė![]() Ö®¼äµÄŗÆŹż¹ŲĻµŹ½ŹĒ
Ö®¼äµÄŗÆŹż¹ŲĻµŹ½ŹĒ![]() £¬
£¬
![]() £¬µĆ
£¬µĆ![]() £¬
£¬
¼“¼×Ģįøß¼Ó¹¤ĖŁ¶Čŗó¼×¼Ó¹¤µÄĮć¼žŹż![]() Óė
Óė![]() Ö®¼äµÄŗÆŹż¹ŲĻµŹ½ŹĒ
Ö®¼äµÄŗÆŹż¹ŲĻµŹ½ŹĒ![]() £Ø
£Ø![]() £©£»
£©£»
£Ø3£©µ±¼×”¢ŅŅĮ½ČĖĻą²ī12øöĮć¼žŹ±£¬¼×¼Ó¹¤Įć¼žµÄŹ±¼äŹĒ![]() Ź±”¢
Ź±”¢![]() Ź±»ņ
Ź±»ņ![]() Ź±£¬
Ź±£¬
ĄķÓÉ£ŗĮī![]() £¬
£¬
½āµĆ£¬![]() £¬
£¬![]() £¬
£¬
Įī![]() £¬
£¬
½āµĆ£¬![]()
¼“µ±¼×”¢ŅŅĮ½ČĖĻą²ī12øöĮć¼žŹ±£¬¼×¼Ó¹¤Įć¼žµÄŹ±¼äŹĒ![]() Ź±”¢
Ź±”¢![]() Ź±»ņ
Ź±»ņ![]() Ź±£®
Ź±£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
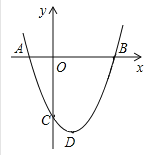
”¾ĢāÄæ”æŅŃÖŖČēĶ¼£¬Å×ĪļĻߵĶ„µćDµÄ×ų±źĪŖ£Ø1£¬-4£©£¬ĒŅÓėyÖį½»ÓŚµć
C£Ø0£¬3£©
ĒóøĆŗÆŹżµÄ¹ŲĻµŹ½£»
ĒóøÄÅ×ĪļĻßÓėxÖįµÄ½»µćA£¬BµÄ×ų±ź.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
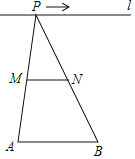
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖĻ߶Ī![]() £¬
£¬![]() ŹĒÖ±Ļß
ŹĒÖ±Ļß![]() ÉĻŅ»¶Æµć£¬µć
ÉĻŅ»¶Æµć£¬µć![]() £¬
£¬![]() ·Ö±šĪŖ
·Ö±šĪŖ![]() £¬
£¬![]() µÄÖŠµć£¬¶ŌĻĀĮŠø÷Öµ£ŗ¢ŁĻ߶Ī
µÄÖŠµć£¬¶ŌĻĀĮŠø÷Öµ£ŗ¢ŁĻ߶Ī![]() µÄ³¤£»¢Ś
µÄ³¤£»¢Ś![]() µÄÖܳ¤£»¢Ū
µÄÖܳ¤£»¢Ū![]() µÄĆ껿£»¢ÜÖ±Ļß
µÄĆ껿£»¢ÜÖ±Ļß![]() £¬
£¬![]() Ö®¼äµÄ¾ąĄė£»¢Ż
Ö®¼äµÄ¾ąĄė£»¢Ż![]() µÄ“󊔣®ĘäÖŠ²»»įĖęµć
µÄ“󊔣®ĘäÖŠ²»»įĖęµć![]() µÄŅĘ¶Æ¶ųøıäµÄŹĒ_____£®£ØĢīŠņŗÅ£©
µÄŅĘ¶Æ¶ųøıäµÄŹĒ_____£®£ØĢīŠņŗÅ£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijĒųŌŚŹµŹ©¾ÓĆńÓĆĖ®¶ī¶Ø¹ÜĄķĒ°£¬¶Ō¾ÓĆńÉś»īÓĆĖ®Ēéæö½ųŠŠĮĖµ÷²é£¬ĻĀ±ķŹĒĶعż¼ņµ„Ė껜³éŃł»ńµĆµÄ50øö¼ŅĶ„Č„ÄźŌĀĘ½¾łÓĆĖ®Įæ£Øµ„Ī»£ŗ¶Ö£©£¬²¢½«µ÷²éŹż¾Ż½ųŠŠČēĻĀÕūĄķ£ŗ
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
ʵŹż·Ö²¼±ķ
·Ö×é | »®¼Ē | ʵŹż |
2.0£¼x”Ü3.5 | ÕżÕż | 11 |
3.5£¼x”Ü5.0 |
| 19 |
5.0£¼x”Ü6.5 | ||
6.5£¼x”Ü8.0 | ||
8.0£¼x”Ü9.5 |
| 2 |
ŗĻ¼Ę | 50 |
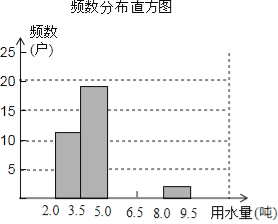
£Ø1£©°ŃÉĻĆęʵŹż·Ö²¼±ķŗĶʵŹż·Ö²¼Ö±·½Ķ¼²¹³äĶźÕū£»
£Ø2£©“ÓÖ±·½Ķ¼ÖŠÄćÄܵƵ½Ź²Ć“ŠÅĻ¢£æ£ØŠ“³öĮ½Ģõ¼“æÉ£©£»
£Ø3£©ĪŖĮĖ¹ÄĄų½ŚŌ¼ÓĆĖ®£¬ŅŖČ·¶ØŅ»øöÓĆĖ®ĮæµÄ±ź×¼£¬³¬³öÕāøö±ź×¼µÄ²æ·Ö°“1.5±¶¼ŪøńŹÕ·Ń£¬ČōŅŖŹ¹60%µÄ¼ŅĶ„ŹÕ·Ń²»ŹÜÓ°Ļģ£¬Äć¾õµĆ¼ŅĶ„ŌĀ¾łÓĆĖ®ĮæÓ¦øƶØĪŖ¶ąÉŁ£æĪŖŹ²Ć“£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗŌŚ¾ŲŠĪABCDÖŠ£¬AD£½2AB£¬µćEŌŚÖ±ĻßADÉĻ£¬Į¬½ÓBE£¬CE£¬ČōBE£½AD£¬Ōņ”ĻBECµÄ“óŠ”ĪŖ_____¶Č£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
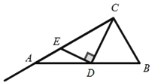
”¾ĢāÄæ”æČēĶ¼£¬ŌŚABCÖŠ£¬ACB 90£¬BAC 30£¬ AB2£¬DŹĒAB±ßÉĻµÄŅ»øö¶Æµć£ØµćD²»ÓėµćA”¢BÖŲŗĻ£©£¬Į¬½ÓCD£¬¹żµćD×÷CDµÄ“¹Ļß½»ÉäĻßCAÓŚµćE£®µ±ADEĪŖµČŃüČż½ĒŠĪŹ±£¬ADµÄ³¤¶ČĪŖ__________£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪOABCÖŠ£¬AO=10£¬AB=8£¬ŃŲÖ±ĻßCDÕŪµž¾ŲŠĪOABCµÄŅ»±ßBC£¬Ź¹µćBĀäŌŚOA±ßÉĻµÄµćE“¦£®·Ö±šŅŌOC£¬OAĖłŌŚµÄÖ±ĻßĪŖxÖį£¬yÖį½ØĮ¢Ę½ĆęÖ±½Ē×ų±źĻµ£¬Å×ĪļĻßy=ax2+bx+c¾¹żO£¬D£¬CČżµć£®
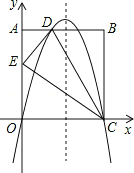
£Ø1£©ĒóADµÄ³¤¼°Å×ĪļĻߵĽāĪöŹ½£»
£Ø2£©Ņ»¶ÆµćP“ÓµćE³ö·¢£¬ŃŲECŅŌĆæĆė2øöµ„Ī»³¤µÄĖŁ¶ČĻņµćCŌĖ¶Æ£¬Ķ¬Ź±¶ÆµćQ“ÓµćC³ö·¢£¬ŃŲCOŅŌĆæĆė1øöµ„Ī»³¤µÄĖŁ¶ČĻņµćOŌĖ¶Æ£¬µ±µćPŌĖ¶Æµ½µćCŹ±£¬Į½µćĶ¬Ź±Ķ£Ö¹ŌĖ¶Æ£®ÉčŌĖ¶ÆŹ±¼äĪŖtĆė£¬µ±tĪŖŗĪÖµŹ±£¬ŅŌP”¢Q”¢CĪŖ¶„µćµÄČż½ĒŠĪÓė”÷ADEĻąĖĘ£æ
£Ø3£©µćNŌŚÅ×ĪļĻ߶Ō³ĘÖįÉĻ£¬µćMŌŚÅ×ĪļĻßÉĻ£¬ŹĒ·ń“ęŌŚÕāŃłµÄµćMÓėµćN£¬Ź¹ŅŌM£¬N£¬C£¬EĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćMÓėµćNµÄ×ų±ź£Ø²»Š“Ēó½ā¹ż³Ģ£©£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ”÷ABCÖŠ£¬”ĻBAC=90![]() £¬AB=AC.µćDĪŖÖ±ĻßBCÉĻŅ»¶Æµć£ØµćD²»ÓėµćB”¢CÖŲŗĻ£©£¬ŅŌADĪŖÖ±½Ē±ßŌŚADÓŅ²ą×÷µČŃüÖ±½ĒČż½ĒŠĪADE£¬Ź¹
£¬AB=AC.µćDĪŖÖ±ĻßBCÉĻŅ»¶Æµć£ØµćD²»ÓėµćB”¢CÖŲŗĻ£©£¬ŅŌADĪŖÖ±½Ē±ßŌŚADÓŅ²ą×÷µČŃüÖ±½ĒČż½ĒŠĪADE£¬Ź¹![]() DAE=90
DAE=90![]() £¬Į¬½įCE.
£¬Į¬½įCE.
Ģ½¾æ£ŗČēĶ¼¢Ł£¬µ±µćDŌŚĻ߶ĪBCÉĻŹ±£¬Ö¤Ć÷BC=CE+CD.
Ó¦ÓĆ£ŗŌŚĢ½¾æµÄĢõ¼žĻĀ£¬ČōAB=![]() £¬CD=1£¬Ōņ”÷DCEµÄÖܳ¤ĪŖ_______.
£¬CD=1£¬Ōņ”÷DCEµÄÖܳ¤ĪŖ_______.
ĶŲÕ¹£ŗ(1)ČēĶ¼¢Ś£¬µ±µćDŌŚĻ߶ĪCBµÄŃÓ³¤ĻßÉĻŹ±£¬BC”¢CD”¢CEÖ®¼äµÄŹżĮæ¹ŲĻµĪŖ_______.
(2)ČēĶ¼¢Ū£¬µ±µćDŌŚĻ߶ĪBCµÄŃÓ³¤ĻßÉĻŹ±£¬BC”¢CD”¢CEÖ®¼äµÄŹżĮæ¹ŲĻµĪŖ_______.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¶ž“ĪŗÆŹż y£½ax2+bx+c£Øa”Ł0£©£¬¹ż£Ø1£¬y1£©£Ø2£¬y2£©£®
¢ŁČō y1£¾0 Ź±£¬Ōņ a+b+c£¾0
¢ŚČō a£½b Ź±£¬Ōņ y1£¼y2
¢ŪČō y1£¼0£¬y2£¾0£¬ĒŅ a+b£¼0£¬Ōņ a£¾0
¢ÜČō b£½2a©1£¬c£½a©3£¬ĒŅ y1£¾0£¬ŌņÅ×ĪļĻߵĶ„µćŅ»¶ØŌŚµŚČżĻóĻŽÉĻŹöĖÄøöÅŠ¶ĻÕżČ·µÄÓŠ£Ø £©øö£®
A. 1 B. 2 C. 3 D. 4
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com