
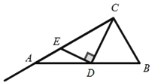
【题目】如图,在ABC中,ACB 90,BAC 30, AB2,D是AB边上的一个动点(点D不与点A、B重合),连接CD,过点D作CD的垂线交射线CA于点E.当ADE为等腰三角形时,AD的长度为__________.
【答案】1或![]()
【解析】
分两种情况:①当点E在AC上,AE=DE时,则∠EDA=∠BAC=30°,由含30°角的直角三角形的性质得出BC=1,∠B=60°,证出△BCD是等边三角形,得出AD=AB-BD=1;②当点E在射线CA上,AE=AD时,得出∠E=∠ADE=15°,由三角形内角和定理求出∠ACD=∠CDA,由等角对等边得出AD=AC=![]() 即可.
即可.
解:分两种情况:①当点E在AC上,AE=DE时,
∴∠EDA=∠BAC=30°,
∵DE⊥CD,
∴∠BDC=60°,
∵∠ACB=90°,∠BAC=30°,
∴BC=![]() AB=1,∠B=60°,
AB=1,∠B=60°,
∴△BCD是等边三角形,
∴BD=BC=1,
∴AD=AB-BD=1;
②当点E在射线CA上,AE=AD时,如图所示:
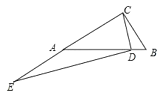
∵∠BAC=30°,
∴∠E=∠ADE=15°,
∵DE⊥CD,
∴∠CDA=90°15°=75°,
∴∠ACD=180°30°75°=75°=∠CDA,
∴AD=AC=![]() ,
,
综上所述:AD的长度为1或![]() ;
;
故答案为:1或![]() .
.


科目:初中数学 来源: 题型:
【题目】类比等腰三角形的定义,我们定义:有三条边相等的凸四边形叫做“准等边四边形”.
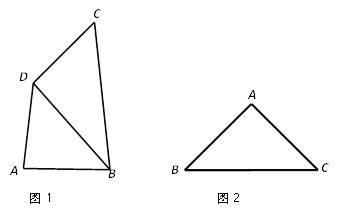
(1)已知:如图1,在“准等边四边形”ABCD中,BC≠AB,BD⊥CD,AB=3,BD=4,求BC的长;
(2)在探究性质时,小明发现一个结论:对角线互相垂直的“准等边四边形”是菱形.请你判断此结论是否正确,若正确,请说明理由;若不正确,请举出反例;
(3)如图2,在△ABC中,AB=AC=![]() ,∠BAC=90°.在AB的垂直平分线上是否存在点P,使得以A,B,C,P为顶点的四边形为“准等边四边形”. 若存在,请求出该“准等边四边形”的面积;若不存在,请说明理由.
,∠BAC=90°.在AB的垂直平分线上是否存在点P,使得以A,B,C,P为顶点的四边形为“准等边四边形”. 若存在,请求出该“准等边四边形”的面积;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1,图2是两张形状、大小完全相同的6×6方格纸,方格纸中的每个小长方形的边长为1,所求的图形各顶点也在格点上.

(1)在图1中画一个以点![]() ,
,![]() 为顶点的菱形(不是正方形),并求菱形周长;
为顶点的菱形(不是正方形),并求菱形周长;
(2)在图2中画一个以点![]() 为所画的平行四边形对角线交点,且面积为6,求此平行四边形周长.
为所画的平行四边形对角线交点,且面积为6,求此平行四边形周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
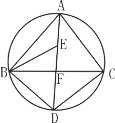
【题目】如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D.AD与BC相交于点F,连结BE,DC,已知EF=2,CD=5,则AD=______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别加工100个零件,甲第1个小时加工了10个零件,之后每小时加工30个零件.乙在甲加工前已经加工了40个零件,在甲加工3小时后乙开始追赶甲,结果两人同时完成任务.设甲、乙两人各自加工的零件数为![]() (个),甲加工零件的时间为
(个),甲加工零件的时间为![]() (时),
(时),![]() 与
与![]() 之间的函数图象如图所示.
之间的函数图象如图所示.

(1)在乙追赶甲的过程中,求乙每小时加工零件的个数.
(2)求甲提高加工速度后甲加工的零件数![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)当甲、乙两人相差12个零件时,直接写出甲加工零件的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
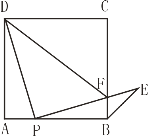
【题目】如图,点P是正方形ABCD边AB上一点(不与点A,B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE, PE交边BC于点F.连接BE、DF.
(1)求证:∠ADP=∠EPB;
(2)求∠CBE的度数;
(3)当![]() 的值等于多少时.△PFD∽△BFP?并说明理由.
的值等于多少时.△PFD∽△BFP?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】徐州至北京的高铁里程约为700km,甲、乙两人从徐州出发,分别乘坐“徐州号”高铁A与“复兴号”高铁B前往北京.已知A车的平均速度比B车的平均速度慢80km/h,A车的行驶时间比B车的行驶时间多40%,两车的行驶时间分别为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,是一个三节段式伸缩晾衣架,如图2,是其衣架侧面示意图,![]() 为衣架的墙角固定端,
为衣架的墙角固定端,![]() 为固定支点,
为固定支点,![]() 为滑动支点,四边形
为滑动支点,四边形![]() 和四边形
和四边形![]() 是菱形,且
是菱形,且![]() ,点
,点![]() 在
在![]() 上滑动时,衣架外延钢体发生角度形变,其外延长度(点
上滑动时,衣架外延钢体发生角度形变,其外延长度(点![]() 和点
和点![]() 间的距离)也随之变化,形成衣架伸缩效果,伸缩衣架为初始状态时,衣架外延长度为
间的距离)也随之变化,形成衣架伸缩效果,伸缩衣架为初始状态时,衣架外延长度为![]() ,当点
,当点![]() 向点
向点![]() 移动
移动![]() 时,外延长度为
时,外延长度为![]() .
.

(1)则菱形![]() 的边长为______
的边长为______![]() .
.
(2)如图3,当![]() 时,
时,![]() 为对角线(不含
为对角线(不含![]() 点)上任意一点,则
点)上任意一点,则![]() 的最小值为______.
的最小值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
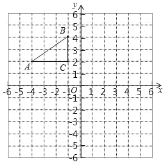
【题目】在平面直角坐标系中,Rt△ABC 的三个顶点分别是 A(﹣4,2),B(﹣1,4),C(﹣1,2).
(1)将△ABC 以点 C 为旋转中心旋转 180°,画出旋转后对应的△![]() ,
,![]() 的坐标为 ;
的坐标为 ;
(2)平移△ABC,点 B 的对应点 ![]() 的坐标为(4,﹣1),画出平移后对应的△
的坐标为(4,﹣1),画出平移后对应的△![]() ,
,![]() 的坐标为 ;
的坐标为 ;
(3)若将△![]() 绕某一点旋转可以得到△
绕某一点旋转可以得到△![]() ,请直接写出旋转中心的坐标 为 .
,请直接写出旋转中心的坐标 为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com