
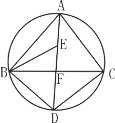
【题目】如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D.AD与BC相交于点F,连结BE,DC,已知EF=2,CD=5,则AD=______________.
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.

(1)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(2)如图②,若∠CAB=60°,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 y=ax2+bx+c(a≠0)中,函数 y 与自变量 x 的部分对应值如下表:
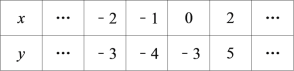
(1)求二次函数的解析式;
(2)求该函数图象与 x 轴的交点坐标;
(3)不等式 ax2+bx+c+3>0 的解集是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区在实施居民用水额定管理前,对居民生活用水情况进行了调查,下表是通过简单随机抽样获得的50个家庭去年月平均用水量(单位:吨),并将调查数据进行如下整理:
4.7 2.1 3.1 2.3 5.2 2.8 7.3 4.3 4.8 6.7
4.5 5.1 6.5 8.9 2.2 4.5 3.2 3.2 4.5 3.5
3.5 3.5 3.6 4.9 3.7 3.8 5.6 5.5 5.9 6.2
5.7 3.9 4.0 4.0 7.0 3.7 9.5 4.2 6.4 3.5
4.5 4.5 4.6 5.4 5.6 6.6 5.8 4.5 6.2 7.5
频数分布表
分组 | 划记 | 频数 |
2.0<x≤3.5 | 正正 | 11 |
3.5<x≤5.0 |
| 19 |
5.0<x≤6.5 | ||
6.5<x≤8.0 | ||
8.0<x≤9.5 |
| 2 |
合计 | 50 |
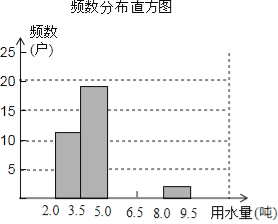
(1)把上面频数分布表和频数分布直方图补充完整;
(2)从直方图中你能得到什么信息?(写出两条即可);
(3)为了鼓励节约用水,要确定一个用水量的标准,超出这个标准的部分按1.5倍价格收费,若要使60%的家庭收费不受影响,你觉得家庭月均用水量应该定为多少?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
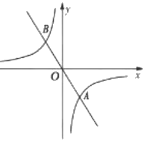
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y= -2x和反比例函数![]() 的图象交于A(a,-4),B两点。过原点O的另一条直线l与双曲线
的图象交于A(a,-4),B两点。过原点O的另一条直线l与双曲线![]() 交于点P,Q两点(P点在第二象限),若以点A,B,P,Q为顶点的四边形面积为24,则点P的坐标是_______
交于点P,Q两点(P点在第二象限),若以点A,B,P,Q为顶点的四边形面积为24,则点P的坐标是_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABC中,ACB 90,BAC 30, AB2,D是AB边上的一个动点(点D不与点A、B重合),连接CD,过点D作CD的垂线交射线CA于点E.当ADE为等腰三角形时,AD的长度为__________.
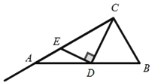
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,吊车在水平地面上吊起货物时,吊绳BC与地面保持垂直,吊臂AB与水平线的夹角为64°,吊臂底部A距地面1.5m.(计算结果精确到0.1m,参考数据sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)
(1)当吊臂底部A与货物的水平距离AC为5m时,吊臂AB的长为 m.
(2)如果该吊车吊臂的最大长度AD为20m,那么从地面上吊起货物的最大高度是多少?(吊钩的长度与货物的高度忽略不计)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com